Калькулятор уклонов — посчитать онлайн
Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Посчитать уклон
Посчитать превышение
Посчитать расстояние
Просто введите значения и выберите единицы измерения уклона.
Теория
Как посчитать уклон
Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:
В процентах:
Уклон в % = h / L ⋅ 100
В промилле:
Уклон в ‰ = h / L ⋅ 1000
В градусах:
Уклон в ° = arctg(h/L)
Пример
Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:
Уклон дороги = 30/500 ⋅ 100 = 6%
Как посчитать превышение
Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
h = L ⋅ Уклон в % /100
Если уклон в промилле (‰):
h = L ⋅ Уклон в ‰ /1000
Если уклон в градусах (°):
h = L ⋅ tg(α) , где α — уклон в градусах
Пример
Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:
h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м
Как посчитать расстояние
Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
L = h / Уклон в % ⋅ 100
Если уклон в промилле (‰):
L = h / Уклон в ‰ ⋅ 1000
Если уклон в градусах (°):
L = h / tg(α), где α — уклон в градусах
Пример
Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:
L = 6 / 30 ⋅1000 = 200 м
См. также
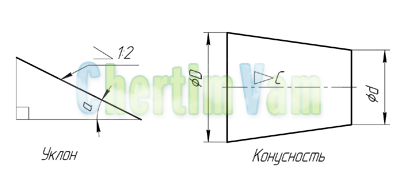
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
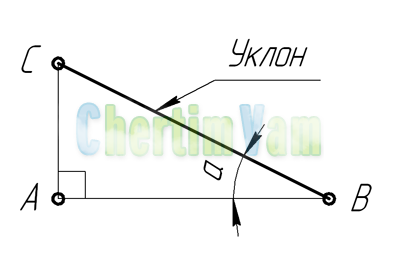
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
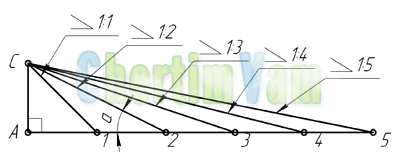
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
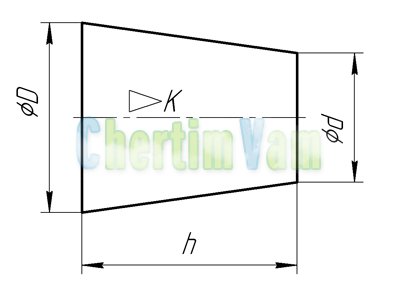
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
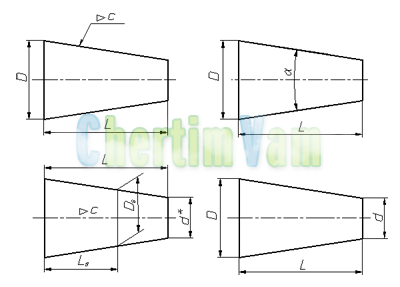
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

С каждым годом при строительстве частных домов предъявляются все более жесткие требования к качеству, эргономичности и практичности отдельных конструкций. Лестница является наиболее используемым элементом в любом многоэтажном доме и в этой статье мы постараемся ответить на вопрос, как подобрать наиболее оптимальный угол наклона марша, для того чтобы эксплуатация изделия была наиболее комфортной и не сопровождалась трудностями при перемещении между ярусами.
Содержание
Что такое угол наклона лестницы?
Угол наклона лестницы – это угол наклона лестничного марша по отношению к поверхности пола. Соответственно, чем меньше числовое значение угла, тем более пологая конструкция получается.
Небольшой угол подъема позволяет подобрать наиболее оптимальную ширину проступи и высоту ступени, что в свою очередь обеспечивает более высокий уровень безопасности при эксплуатации пожилыми, детьми и людьми с ограниченными возможностями.
Главным недостатком такого типа конструкции является чрезвычайная массивность и громоздкость – не в каждом доме найдется свободное пространство под такое сооружение, а если и найдется, то без необходимости, редко кто готов так неэффективно использовать жилую площадь.
Также не рекомендуется устанавливать слишком крутую конструкцию, так как она накладывает определенные физические ограничения на жильцов. Из-за высоких ступеней перемещаться по такой лестнице будет проблематично, утомительно и зачастую небезопасно.
Нас часто спрашивают: уклон лестницы 1:1 – что это значит и сколько это ? Ответ крайне прост – уклон 1:1 равен углу в 45 градусов, т.е. глубина ступени фактически равна ее высоте. Уклон 1:2 – это угол в 27,5 градусов, т.е. глубина ступени в два раза больше ее высоты.
Оптимальный угол наклона лестницы
Для определения оптимального угла наклона лестничного марша ориентируются на строительные нормативы, технические особенности помещения и конечно же, личные предпочтения.
Считается, что в частном домостроении для повседневного использования наиболее приемлемым является уклон в 45 градусов, оптимальным 35-45 градусов, а идеальным – 30-35. В этих случаях, при использовании лестницы человек будет прилагать наименьшие усилия при перемещении и у него не возникнет чувство дискомфорта.
Тем не менее не всегда рационально использовать именно такие уклоны. В зависимости от назначения и места установки, ориентироваться стоит на другие рекомендованные значения.

Например, разбив все конструкции на несколько групп можно определить оптимальные углы наклона:
- Пандусы . Используются при наличии людей с ограниченными возможностями. Обязательно должны быть пологими с углами не более 15 градусов.
- Уличные и садовые лестницы. Применяются в общественных пространствах, парках, садах. Должны обеспечивать комфортный подъем для широкого круга людей, поэтому наклон не должен быть значительным – до 30 градусов.
- Внутренние лестницы. Используются в многоквартирных и частных домах. Считается что лестница с уклоном от 30 до 45 градусов является наиболее оптимальной, так обеспечивает комфортное перемещение для среднестатистического человека и не занимает большую площадь.
- Чердачные лестницы. В случаях, когда невозможно и/или нецелесообразно установить классическую лестничную конструкцию, применяются крутые, но компактные чердачные лестницы с углом до 60 градусов.
- Стремянки, трапы, пожарные лестницы. Приставные лестницы являются временным решением и используются крайне редко, они устанавливаются с минимальным уклоном, т.е. практически вертикально.
Не забывайте, что главным критерием при выборе угла наклона лестницы должны быть потребности проживающих в доме людей, так как именно им придется использовать конструкцию в наибольшей степени.
Какие показатели влияют на уклон лестницы?
Как уже было не раз отмечено, что на показатель уклона лестницы влияют ширина и высота ступеней. Низкие ступени и широкая проступь обеспечивают более пологую, но в то же время более громоздкую конструкцию, соответственно, более высокие и узкие ступени позволяют использовать меньшее пространство, так как увеличивается максимальный угол подъема лестницы.
Считается, что оптимальным показателем высоты ступени является 15-18 см. Более высокое значение приводит к возникновению трудностей при перемещении, а меньшее к нецелесообразному укрупнению сооружения.
Ширина проступи определяет непосредственно эффективную глубину ступенек. Подбирается на основании средней длины шага пользователей и технических возможностей помещения. Рекомендованная ширина 27-30 см.

Почти все конструктивные особенности изделия определяет ГОСТ 23120-78 «Лестницы маршевые, площадки и ограждения».
Как рассчитать угол наклона лестницы?
Расчет угла наклона лестничного марша является одной из самых важных задач при проектировании конструкции, так как именно этот параметр предопределяет характеристики остальных элементов сооружения. Мы предлагаем вам ознакомиться с двумя методами расчета – автоматизированный с помощью онлайн-калькулятора и классический ручной.
Расчет угла наклона лестницы – Онлайн калькулятор
Если вы боитесь ошибиться и у вас нет лишнего времени, лучшим решением для того чтобы рассчитать угол наклона лестницы на второй этаж станут наши надежные онлайн-калькуляторы. У нас доступен расчет следующих типов конструкций:
- прямая лестница на тетивах;
- прямая лестница на косоурах;
- прямая лестница с ломаным косоуром;
- лестница на косоурах с забежными ступенями с поворотом на 90;
- лестница на косоурах с забежными ступенями с поворотом на 180;
- одномаршевая лестница на косоурах с площадкой с поворотом на 90;
- двухмаршевая лестница на косоурах с площадкой с поворотом на 180;
- трехмаршевая лестница на косоурах с площадкой с поворотом на 180.
Перейдите на страницу интересующей лестницы, введите необходимые параметры проема и нажмите кнопку «Рассчитать».
Вам будет доступен блок с результатами расчета, в котором вы можете подчерпнуть большое количество полезной информации – практически готовую смету. В отдельном окне выводятся чертежи, схемы и 3D-модель конструкции.


Расчет наклона лестницы вручную
Классическим, но не всегда рациональным методом является расчет угла лестницы вручную. Мы покажем, как применяя простые геометрические правила можно определить искомое значение и разберем пример.
Существует два основных способа расчета:
- Способ #1 – наиболее простой. Зная параметры глубины и высоты ступени, вы можете сразу определить угол наклона лестницы, так как фактически он будет совпадать с углом наклона гипотенузы прямоугольного треугольника, образованного ступенями. Для того чтобы его определить нужно знать тангенс угла А.

Формула расчета угла наклона лестницы: tg(A) = h / s
- Способ #2. Суть расчета сводится к тому же, только здесь в качестве катетов прямоугольного треугольника выступает высота и длина проема. Рассмотрим второй случай, как наиболее подробный.
Считается, что максимально комфортными и удобными лестницами являются те, при ходьбе на которых не приходится искусственно изменять привычную длину шага. У каждого человека свой стандарт, однако среднее значение находится в пределах 60-65 см. Вы можете измерить свой, а мы продолжим пример с размером равным 63 см.

Рекомендованные значения ширины проступи и высоты ступеней мы уже обсуждали, но как понять какое именно значение подобрать из этих интервалов.
Опытным путем специалисты выяснили, что длина шага равна сумме глубины проступи и двойной высоте ступеней. То же самое можно записать в виде формулы:
Формула расчета ступеней: 2 × h + s = 60/65 см
Т.е. зная длину шага человека и допустимые интервалы, можно подобрать наиболее комфортные параметры ступеней. Перебрав все возможные варианты, у нас получились найти две пары теоретических значений: s = 27 см и h = 18 см или s = 29 см и h = 17 см. Возьмем первую.
Для тех, кто не хочет углубляться в подробности, можно остановиться на формуле tg(A) = h / s и закончить расчет прямо сейчас.
Далее нам необходимо определить высоту этажа. Мы возьмем стандартный потолок для частного дома – 270 см и прибавим толщину перекрытия с конструкцией пола верхнего этажа, в среднем, это составляет 30 см. Вам же необходимо измерить рулеткой фактическое значение и в дальнейших расчетах использовать именно его.
Зная высоту этажа и высоту ступеней, мы можем определить их количество:
300 см / 18 см = 16,7 ступеней.
Так как число получилось не целое, округлим в большую сторону (до 17) и произведем обратный расчет, для определения точной высоты ступеней.
300 см / 17 = 17,6 см.
Теперь вернемся к первоначальной формуле и рассчитаем реальную ширину проступи по известной высоте ступеней.
63 см – 17,6 см × 2 = 27,8 см.
У нас получилось, что h = 17,6 см, s = 27,8 см – оба значение соответствуют рекомендуемым, значит можно продолжить расчет.
Так как мы рассчитываем пример для наглядности – для упрощения расчетов мы округляем сотые доли полученных значений. В реальной ситуации, так делать не рекомендуется .
Дальше определим длину лестницы в горизонтальной проекции на основании данных по количеству ступеней и их длине.
17 × 27,8 см = 472,6 см.
После проведения вычислений вам необходимо убедиться в наличии необходимого пространства для монтажа лестницы. Если такового нет (что часто случается), необходимо выполнить расчет в обратную сторону, отталкиваясь не от оптимального угла наклона лестницы, а от возможностей помещения.
Также следует рассмотреть многомаршевые конструкции. Для них расчет проводится аналогично, только для каждого марша в отдельности.
Но предположим, что у вас имеется необходимая площадь, тогда заключительный этап работ сводится к определению тангенса угла, образованного длиной и высотой проема.

В этом случае, оптимальный угол наклона лестницы будет равен:
tg(α) = 300 / 472,6 = 0,63
α = arctg(0,63) = 32.2°
У нас получилась идеальная лестница , так как мы заранее взяли идеальные размеры ступеней, но из-за ограниченных размеров помещения, чаще всего так не получается и приходится увеличивать угол.
Например, если мы возьмем максимальный угол наклона лестницы в 40 градусов, то длину проема можно уменьшить до 357 см.
tg(40°) ≈ 0,84
0,84 = 300 см / x см
x ≈ 357 см
Манипуляции с длиной проема и углом наклона лестницы непременно приведут к изменению параметров ступеней и скорее всего они выйдут из диапазона комфортных, но если помещение технически не может вместить лестницу – другого выбора нет.
Помните, что грамотно выполненный расчет угла наклона лестницы – это единственно верный путь к удобству и безопасности при эксплуатации. Доверьте свои расчеты нашим надежным калькуляторам лестниц и будьте уверены в своей конструкции!
Как начертить уклоны и конусность
Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.
Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307—68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.
Конусностью называют отношение диаметра основания конуса к его высоте. В этом случае конусность К=d/l. Для усеченного конуса К = (d-d1)/l. Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l1 — длина конической части — 42 мм; d1 — наружный диаметр резьбы — 16 мм; К — конусность 1 : 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.
n
n
TBegin—>TEnd—>
n
n
Рис. 1. Построение уклонов
n
n
Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593—57 .
n
n
n
n
Рис. 2. Пример построения уклонов
n
n
TBegin—>TEnd—>
n
n
Рис. 3. Построение конусности
n
Уклон в процентах и промилле
Угол уклона — показатель наклона какой либо поверхности (дороги, крыши, пандуса, лестничного марша и пр.) относительно уровня горизонта.Угловые размеры указывают на чертежах в градусах, минутах и секундах с обозначением единицы измерения (ГОСТ 2.307-2011 «Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений«).
В соответствии с ГОСТ Р 21.1101-2013 «Система проектной документации для строительства (СПДС). Основные требования к проектной и рабочей документации», на планах направление уклона плоскостей указывают стрелкой, над которой при необходимости проставляют числовое значение уклона в процентах или в виде отношения единицы высоты плоскости к соответствующей горизонтальной проекции. Допускается числовое значение уклона указывать в промилле или в виде десятичной дроби с точностью до третьего знака.
острый угол которого должен быть направлен в сторону уклона (кроме крутизны откосов насыпей и выемок). Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
Также вместо знака угла, на чертежах встречается и буквенное обозначение уклона ( i ).
В процентах обычно обозначают углы уклонов крыш, пандусов, лестничных маршей и т.п.
В промилле обозначают углы уклонов плоскостных сооружений — спортивные игровые площадки, поля, беговые дорожки, а также линейные сооружения — автомобильные и железные дороги.
Процент ( % ) — одна сотая доля.
Промилле ( ‰ ) — одна тысячная доля.
Например: уклон при высоте 0,2 метра и протяженностью по горизонтали 4 метра будет равен 5 % (читается как — пять сотых) или 50 ‰ (читается как — пятьдесят тысячных), это значение также будет соответствовать приблизительно — 3 о.
Чертеж 1
Часто спрашивают, что означает уклон, на пример 0,05 — это соотношение высоты к длине горизонтального участка (0,2 м / 4 м = 0,05 — см. чертеж 1), которое при необходимости можно перевести в проценты или промилле, смотря что требуется.
Для определение угла уклона в процентах (%) (см. чертеж 1) необходимо: 0,2 м / 4 м х 100 = 5 %.
Для определение угла уклона в промилле (‰) необходимо: 0,2 м / 4 м х 1000 = 50 ‰.
Ту же величину уклона можно обозначить и как соотношение высоты к длине горизонтального участка — 1:20 (4 / 0,2 = 20).
Если требуется определить протяженность горизонтального участка, зная величину уклона в процентах и его высоту из чертежей, необходимо — 0,2 м / (5 % / 100) = 4 м.
Чтобы определить высоту уклона, зная величину уклона в процентах и протяженность участка из чертежей, необходимо — 5 % / 100 х 4 м = 0,2 м.
Аналогичным образом вычисляются размеры для угла уклона выраженного в промилле, только вместо деления на 100, выполняется деление на 1000.
Примечание: для того чтобы ввести на компьютере символ промилле (‰), необходимо включить NumLock, нажать клавишу Alt и удерживая ее набрать на цифровом блоке клавиатуры 0137, отпустить клавишу Alt после чего появится символ ‰.
Если требуется определить уклон с точностью до 1 градуса, нужно: 0,2 м / 4 м = 0,05. Полученное число — 0,05 необходимо найти в таблице tg (тангенсов) для углов. Приближенное значение в таблице — 0,0524, будет соответствовать углу 3 о (см. таблицу).
Полная таблица тангенсов для углов от 0о до 360о
Таблица уклонов кровли | Xatki.by
Уклон кровли — показатель крутизны ската крыши. Вычисляется как отношение высоты конька (H) к горизонтальной его проекции (заложению) (l). Иными словами, величина уклона равна тангенсу угла между поверхностью ската и горизонтальной его проекцией.
Итак, уклон рассчитывается по формуле: i=H/l
Для примера дано:
Высота конька (H): 2 м
Заложение (l): 2,86 м
Рассчитаем угол кровли (i): 2/2,86 = 0,699, что близко соответствует 35° по нижеприведенной таблице.
Уклон можно выразить в градусах, процентах, как отношение сторон, как абсолютный уклон, и как коэффициент уклона.
Предложенная таблица поможет вам быстро перевести значения из одной меры в другую.
| Градусы | Проценты (%) | Отношение | Уклон (i) | Коэфф. уклона (К) |
|---|---|---|---|---|
| 4 | 6,99 | 1:14,31 | 0,0699 | 1,003 |
| 5 | 8,75 | 1:11,43 | 0,0875 | 1,004 |
| 6 | 10,51 | 1:9,52 | 0,1051 | 1,006 |
| 7 | 12,28 | 1:8,14 | 0,1228 | 1,008 |
| 8 | 14,05 | 1:7,12 | 0,1405 | 1,010 |
| 9 | 15,84 | 1:6,31 | 0,1584 | 1,012 |
| 10 | 17,63 | 1:5,67 | 0,1763 | 1,015 |
| 11 | 19,44 | 1:5,14 | 0,1944 | 1,019 |
| 12 | 21,26 | 1:4,70 | 0,2126 | 1,022 |
| 13 | 23,09 | 1:4,33 | 0,2309 | 1,027 |
| 14 | 24,93 | 1:4,00 | 0,2493 | 1,031 |
| 15 | 26,79 | 1:3,73 | 0,2679 | 1,035 |
| 16 | 28,67 | 1:3,49 | 0,2867 | 1,040 |
| 17 | 30,57 | 1:3,27 | 0,3057 | 1,046 |
| 18 | 32,49 | 1:3,08 | 0,3249 | 1,051 |
| 19 | 34,43 | 1:2,90 | 0,3443 | 1,058 |
| 20 | 36,4 | 1:2,75 | 0,3640 | 1,064 |
| 21 | 38,39 | 1:2,61 | 0,3839 | 1,071 |
| 22 | 40,4 | 1:2,48 | 0,4040 | 1,079 |
| 23 | 42,45 | 1:2,36 | 0,4245 | 1,086 |
| 24 | 44,52 | 1:2,25 | 0,4452 | 1,095 |
| 25 | 46,63 | 1:2,15 | 0,4663 | 1,104 |
| 26 | 48,77 | 1:2,05 | 0,4877 | 1,113 |
| 27 | 50,95 | 1:1,96 | 0,5095 | 1,122 |
| 28 | 53,17 | 1:1,88 | 0,5317 | 1,133 |
| 29 | 55,43 | 1:1,80 | 0,5543 | 1,143 |
| 30 | 57,74 | 1:1,73 | 0,5774 | 1,155 |
| 31 | 60,09 | 1:1,66 | 0,6009 | 1,167 |
| 32 | 62,49 | 1:1,60 | 0,6249 | 1,179 |
| 33 | 64,94 | 1:1,54 | 0,6494 | 1,192 |
| 34 | 67,45 | 1:1,48 | 0,6745 | 1,206 |
| 35 | 70,02 | 1:1,43 | 0,7002 | 1,221 |
| 36 | 72,65 | 1:1,38 | 0,7265 | 1,236 |
| 37 | 75,36 | 1:1,33 | 0,7536 | 1,252 |
| 38 | 78,13 | 1:1,28 | 0,7813 | 1,269 |
| 39 | 80,98 | 1:1,24 | 0,8098 | 1,287 |
| 40 | 83,91 | 1:1,19 | 0,8391 | 1,305 |
| 41 | 86,93 | 1:1,15 | 0,8693 | 1,325 |
| 42 | 90,04 | 1:1,11 | 0,9004 | 1,346 |
| 43 | 93,25 | 1:1,07 | 0,9325 | 1,367 |
| 44 | 96,57 | 1:1,04 | 0,9657 | 1,390 |
| 45 | 100 | 1:1 | 1 | 1,414 |
| 46 | 103,55 | 1:0,97 | 1,0355 | 1,439 |
| 47 | 107,24 | 1:0,93 | 1,0724 | 1,466 |
| 48 | 111,06 | 1:0,90 | 1,1106 | 1,495 |
| 49 | 115,04 | 1:0,87 | 1,1504 | 1,524 |
| 50 | 119,18 | 1:0,84 | 1,1918 | 1,556 |
| 51 | 123,49 | 1:0,81 | 1,2349 | 1,589 |
| 52 | 127,99 | 1:0,78 | 1,2799 | 1,624 |
| 53 | 132,7 | 1:0,75 | 1,3270 | 1,662 |
| 54 | 137,64 | 1:0,73 | 1,3764 | 1,701 |
| 55 | 142,82 | 1:0,70 | 1,4282 | 1,743 |
| 56 | 148,26 | 1:0,67 | 1,4826 | 1,788 |
| 57 | 153,99 | 1:0,65 | 1,5399 | 1,836 |
| 58 | 160,03 | 1:0,63 | 1,6003 | 1,887 |
| 59 | 166,43 | 1:0,60 | 1,6643 | 1,942 |
| 60 | 173,2 | 1:0,58 | 1,7320 | 2,000 |
| 61 | 180,4 | 1:0,55 | 1,8040 | 2,063 |
| 62 | 188,1 | 1:0,53 | 1,8810 | 2,130 |
| 63 | 196,3 | 1:0,51 | 1,9630 | 2,203 |
| 64 | 205,0 | 1:0,49 | 2,0500 | 2,281 |
| 65 | 214,5 | 1:0,47 | 2,1450 | 2,366 |
| 66 | 224,6 | 1:0,45 | 2,2460 | 2,459 |
| 67 | 235,6 | 1:0,42 | 2,3560 | 2,560 |
| 68 | 247,5 | 1:0,40 | 2,4750 | 2,670 |
| 69 | 260,5 | 1:0,38 | 2,6050 | 2,790 |
| 70 | 274,7 | 1:0,36 | 2,7470 | 2,924 |
| 72 | 307,8 | 1:0,33 | 3,0780 | 3,236 |
| 74 | 348,7 | 1:0,29 | 3,4870 | 3,628 |
Под перфорированными лотками обычно подразумевают металлические кабельные лотки с перфорацией. Кабельный лоток — это конструкция, незаменимая при монтаже энергосистем, поскольку позволяет облегчить прокладку кабеля. Производится она обычно из металла, который обработан антикоррозийным покрытием. В них прокладывают кабельные магистрали, состоящие из большого количества проводов. Они монтируются на стену или потолок, обеспечивают горизонтальную и вертикальную прокладку и множество вариантов креплений. В перфорированных есть отверстия, которые служат нескольким целям:
- улучшают охлаждение кабельной трассы;
- для осмотра кабельных линий не требуется демонтаж;
- снижается вес, что облегчает нагрузку на несущие элементы;
- упрощается сборка и крепление самих лотков, а также кабеля в них.
Подробнее здесь…
Также иногда так называют перфорированные пластиковые кабель-каналы. Они отличаются от обычных гребенчатым профилем боковых участков, что положительно сказывается на общем весе кабельной трассы, упрощает монтаж и снижает стоимость. Другой стороной такой конструкции является снижение защиты содержимого кабельного короба, и низкая возможность вписать кабельный канал в дизайн помещения. Именно поэтому основной областью применения таких коробов является прокладка кабеля в вводно-распределительных устройствах. Распределительные щиты, телекоммуникационные шкафы, щиты управления в таких местах чаще всего применяют перфорированные короба.
Подробнее здесь…
Наклон прямой линии
Purplemath
Одним из наиболее важных свойств прямой является то, как она отклоняется от горизонтали. Эта концепция отражена в том, что называется «уклоном» линии.
Давайте посмотрим на прямую линию y = ( 2 / 3 ) x — 4.Его график выглядит так:
MathHelp.com
Чтобы найти склон, нам понадобятся две точки от линии.
Я выберу два значения x , вставлю их в линейное уравнение и решу для каждого соответствующего значения y . Если, скажем, я выберу x = 3, то:
Теперь допустим, я выбрал x = 9; затем:
(Кстати, я выбрал эти два значения x именно потому, что они были кратны трем; тем самым я знал, что смогу очистить знаменатель дроби, так что я получу хороший результат, аккуратные целые числа для моих полученных и -значений.Это не правило, что вы должны это делать, но это полезный метод.)
Итак, две найденные мной точки (3, –2) и (9, 2) находятся на линии y = ( 2 / 3 ) x — 4.
Чтобы найти уклон, обозначенный « м », мы можем использовать следующую формулу:
(Почему « м » для «склона», а не, скажем, « с »? Официальный ответ: никто не знает.)
В случае, если вы не сталкивались с этими числами ниже, чем переменные, они называются «индексами». Индексы обычно используются для различения похожих вещей или для отсчета, например, в последовательностях. В случае формулы наклона индексы просто указывают, что у нас есть «первая» точка (координаты которой обозначены цифрой «1») и «вторая» точка (координаты которой обозначены цифрой «2»). Другими словами, подписки указывают только на то, что у нас есть два момента, с которыми мы работаем.
(Это зависит только от вас, какой пункт вы обозначите как «первый», а какой — как «второй». Как подсказывает логика, угол линии не изменится только потому, что вы посмотрели на две точки в другой порядок.)
Для вычисления уклонов с формулой уклона важно, чтобы мы тщательно вычитали x и y в в том же порядке . Для наших двух точек, если мы выберем (3, –2) нашей «первой» точкой, то получим следующее:
Первое значение и выше, –2, было взято из точки (3, –2); второе значение и , 2, пришло из точки (9, 2); значения 3 и 9 x были взяты из двух точек в том же порядке .
Если бы, с другой стороны, мы взяли координаты из точек в обратном порядке, результат был бы точно таким же значением:
Как вы можете видеть, порядок, в котором вы перечисляете баллы, действительно не имеет значения, если вы вычитаете значения x в том же порядке, в котором вы вычитали значения и . Из-за этого формула наклона может быть записана так, как это было выше, или, альтернативно, она также может быть записана как:
Позвольте мне подчеркнуть этот момент:
Не имеет значения, какую из двух формул «наклона» вы используете, равно как и то, какую точку вы выбираете как свою «первую», а какую — как «вторую».Важно только то, что для и вы вычитаете свои x -значения в том же порядке , как вычитали свои и -значения.
Для тех, кто заинтересован, эквивалентность двух формул наклона, приведенных выше, может быть доказана, если отметить следующее:
y 1 — y 2 = y 1 + (- y 2 )
= — y 2 + y 1
= — y 1 — (- — y 2 )
= — ( y 2 — y 1 )
Таким же образом:
x 1 — x 2 = x 1 + (- x 2 )
= — x 2 + x 1
= — x 1 — (- x 2 )
= — ( x 2 — x 1 )
Затем первая формула преобразуется во вторую следующим образом:
m = ( y 1 — y 2 ) / ( x 1 — x 2 ) = [- ( y 2 — y 1 )] / [- ( x 2 — x 1 )] = = ( 2 — y 1 ) / ( x 2 — х 1 )
Как вы можете видеть выше, выполнение вычитания в так называемом «неправильном» порядке служит только для создания двух знаков «минус», которые затем удаляются.Итог: не беспокойтесь о том, какой пункт является «первым», потому что это действительно не имеет значения. (И, пожалуйста, не присылайте мне электронное письмо с утверждением, что порядок каким-то образом имеет значение, или что одна из двух вышеприведенных формул как-то «неправильна». Если вы считаете, что я ошибаюсь, вставьте пары точек в обе формулы и попробуй доказать , что я не прав! И продолжай подключать, пока не «увидишь», что математика на самом деле верна.)
Вернемся к строке y = ( 2 / 3 ) x — 4 и найдем еще несколько точек для этого.Если я позволю x = –3, то:
Если я позволю x = 0, то:
Это дает мне две точки, (–3, –6) и (0, –4). Если я нанесу эти две точки на линию, я получу две синие точки, показанные ниже:
Если я поднимусь по лестнице от первой точки ко второй (когда я двигаюсь вправо вдоль оси x ), я получу это:
Следующее, что я буду использовать, это (3, –2).Составляя точку и рисуя ступеньку, я получаю:
Теперь внимательно посмотрите на эти ступеньки. Отсчитайте их от сетки, видимой на заднем плане. Вы увидите, что, переходя от одной точки графика к следующей, я переместился на два шага вверх и на три шага назад. В терминах, знакомых строительной отрасли, эти ступеньки имеют (вертикальный) «подъем» 2 и (горизонтальный) «бег» 3. Когда люди называют «наклон» как «подъем над бегом», это что они имеют в виду.(Для получения дополнительной информации попробуйте здесь.)
Давайте найдем наклон другого уравнения линии:
Найти наклон у = –2 х + 3
График линии, это выглядит так:
Я выберу пару значений для x и найду соответствующие значения для и .Выбор x = –1, я получаю:
y = –2 (–1) + 3 = 2 + 3 = 5
Сбор x = 2, я получаю:
y = –2 (2) + 3 = –4 + 3 = –1
Тогда точки (–1, 5) и (2, –1) находятся на линии y = –2 x + 3. Затем наклон линии вычисляется как:
Кстати, если вы посмотрите на график и начнете с любой точки на линии (для простоты выберите ту, которая также лежит на сетке), вы заметите, что ступенька идет вниз.Вы идете вниз два, более одного; вниз два, более одного; вниз два, более одного. И это соответствует склону, который мы нашли выше:
(меньше двух) / (больше одного) = (–2) / (1) = –2
Найдите наклон линии, проходящей через точки (–3, 5) и (4, –1).
В этом случае мне не нужно находить очки, потому что они уже дали их мне.Так что я сразу перейду к формуле:
м = (5 — (–1)) / (- 3 — 4)
= (5 + 1) / (- 3 + (–4)) = (6) / (- 7)
= — (6/7)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске склона через пару точек.Попробуйте введенное упражнение или введите собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с Mathway. (Или пропустите виджет и продолжите урок.)
(Нажав «Нажмите, чтобы просмотреть шаги», вы попадете прямо на сайт Mathway, если хотите проверить их программное обеспечение или получить дополнительную информацию.)
URL: https: // www.purplemath.com/modules/slope.htm
,Калькулятор уклона
По определению, уклон или уклон линии описывает ее крутизну, уклон или уклон. Где м — уклон |  |

Если 2 очка известны
Если известны 1 точка и уклон
Наклон, иногда называемый в математике градиентом, представляет собой число, которое измеряет крутизну и направление линии или отрезка линии, соединяющей две точки, и обычно обозначается как м. .Как правило, крутизна линии измеряется по абсолютной величине ее уклона м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которое м описывает на основе ее знака и значения:
- Линия увеличивается и идет вверх слева направо, когда m> 0
- Линия уменьшается и идет вниз слева направо, когда m <0
- Линия имеет постоянный наклон и является горизонтальной, когда m = 0
- Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в качестве знаменателя.Обратитесь к уравнению, приведенному ниже.
Склон — это, по сути, изменение высоты по сравнению с изменением горизонтального расстояния, и его часто называют «подъемом по трассе». У этого есть применения в градиентах в географии так же как гражданском строительстве, таком как строительство дорог. В случае дороги «подъем» — это изменение высоты, в то время как «пробег» — это разница в расстоянии между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы можно было учитывать кривизну Земли. как фактор.Наклон представлен математически как:
В приведенном выше уравнении y 2 — y 1 = Δy или вертикальное изменение, а x 2 — x 1 = Δx или горизонтальное изменение, как показано на приведенном графике. Также можно видеть, что Δx и Δy являются отрезками, которые образуют прямоугольный треугольник с гипотенузой d , причем d является расстоянием между точками (x 1 , y 1 ) и (x 2 , y 2 ) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к Треугольному калькулятору для более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , представленный в калькуляторе выше. Кратко:
d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2
Вышеупомянутое уравнение является коренной теоремой Пифагора, в которой гипотенуза d уже решена, а две другие стороны треугольника определяются путем вычитания двух значений x и y , заданных двумя точками ,Учитывая две точки, можно найти θ , используя следующее уравнение:
м = загар (θ)
Учитывая точки (3,4) и (6,8) найти наклон линии, расстояние между двумя точками и угол наклона:
d = √ (6 — 3) 2 + (8 — 4) 2 = 5
Хотя это выходит за рамки данного калькулятора, кроме его основного линейного использования, концепция наклона важна в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой изменяется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
,горизонтальных и вертикальных линий | Purplemath
Purplemath
Давайте снова рассмотрим два уравнения, которые мы сначала сделали на предыдущей странице, и сравним уравнения линий с их значениями наклона.
Уравнение первой линии было y = ( 2 / 3 ) x — 4, а уклон линии составил м = 2 / 3 .
Уравнение второй линии было y = –2 x + 3, а наклон линии был м = –2.
В обоих случаях число, умноженное на переменную x , также было значением наклона для этой линии. Это соотношение всегда выполняется: если уравнение линии имеет вид « y =», то число, умноженное на x , является значением наклона м .
MathHelp.ком

Это соотношение станет очень важным, когда вы начнете работать с линейными уравнениями.
Теперь давайте рассмотрим эти два уравнения и их графики .
Для первого уравнения, y = ( 2 / 3 ) x — 4, уклон составил м = 2 / 3 , положительное число.График выглядел так:
Обратите внимание, как линия, когда мы движемся слева направо по оси x , продвигается вверх к вершине чертежа; технически линия является «возрастающей» линией. И … уклон был положительным.
Это соотношение всегда верно: если линия увеличивается, то ее наклон будет положительным; и если наклон линии положительный, то ее график будет увеличиваться.
Партнерская

Для второй строки, y = –2 x + 3, уклон был m = –2, отрицательное число.График выглядел так:
Обратите внимание на то, как линия, двигаясь слева направо по оси x , смещается вниз к нижней части чертежа; технически линия является «убывающей». И … уклон был отрицательным.
Это соотношение всегда верно: если линия уменьшается, то ее наклон будет отрицательным; и если наклон линии отрицателен, то ее график будет уменьшаться.
Эта связь между знаком на склоне и направлением графика линии может помочь вам проверить ваши расчеты: если вы рассчитываете наклон как отрицательный, но из графика уравнения видно, что линия действительно увеличивается (так что наклон должен быть положительным), тогда вы знаете, что вам нужно пересчитать свои расчеты. Знание этого соединения может сэкономить вам баллы на тесте, потому что оно позволит вам проверить свою работу за до того, как вы сдадите.
Итак, теперь мы знаем: растущие линии имеют положительные наклоны, а убывающие линии имеют отрицательные наклоны. Имея это в виду, давайте рассмотрим следующую горизонтальную линию:
Его график показан ниже:
— горизонтальная линия, окантовывающаяся вверх; то есть это возрастающая линия? Нет, поэтому его наклон не может быть положительным. Горизонтальная линия, окаймленная вниз; то есть это убывающая линия? Нет, поэтому его наклон не может быть отрицательным.Какое число не является ни положительным, ни отрицательным?
Ноль!
Таким образом, наклон этой (и любой другой) горизонтальной линии должен, по логике, быть нулевым. Давайте сделаем расчеты, чтобы подтвердить это. Используя (произвольные) точки линии, (–3, 4) и (5, 4), наклон вычисляется как:
Это соотношение всегда сохраняется: наклон нуля означает, что линия горизонтальна, а горизонтальная линия означает, что вы получите наклон ноль.
(Кстати, все горизонтальные линии имеют вид « y = некоторое число», а уравнение « y = некоторое число» всегда отображается в виде горизонтальной линии.)
Теперь рассмотрим следующую вертикальную линию:
График ниже.
Вертикальная линия идет вверх на одном конце? Ну да, вроде.Так что, возможно, уклон будет положительным …? Вертикальная линия идет вниз на другом конце? Ну, опять же, вроде. Так что может быть наклон будет отрицательным …?
Но есть ли число, которое и положительное, и отрицательное? Нет.
Вердикт: вертикальные линии не имеют наклона. Понятие уклона просто не работает для вертикальных линий. Вертикальный уклон не существует !
Давайте сделаем расчеты, чтобы подтвердить логику.Из графика линии я буду использовать (произвольные) точки (4, 5) и (4, –3). Тогда наклон составляет:
Мы не можем делить на ноль, поэтому, конечно, это значение наклона «неопределено».
Это соотношение всегда верно: вертикальная линия не будет иметь уклона, а «уклон не определен» или «у линии нет уклона» означает, что линия вертикальная.
(Кстати, все вертикальные линии имеют форму « x = некоторое число», а « x = некоторое число» означает, что линия вертикальная).Каждый раз, когда ваша линия имеет неопределенный наклон, линия является вертикальной; и всякий раз, когда линия вертикальная, вы в конечном итоге разделитесь на ноль, если попытаетесь вычислить наклон.)
Предупреждение: очень часто путают эти два типа линий и их наклоны, но они очень разные.
Так же, как «горизонтальный» совсем не то же самое, что «вертикальный», так и «нулевой уклон» совсем не то же самое, что «без уклона».
Точно так же, как «Z» (с двумя горизонтальными линиями) не совпадает с «N» (с двумя вертикальными линиями), так и наклон «Ноль» (для горизонтальной линии) не совпадает с «Нет» «Наклон (для вертикальной линии).
Число «ноль» существует, поэтому горизонтальные линии действительно имеют наклон. Но вертикальные линии не имеют никакого наклона; «Наклон» просто не имеет никакого значения для вертикальных линий.
Очень часто тесты содержат вопросы относительно горизонтали и вертикали. Не путай их!
URL: https://www.purplemath.com/modules/slope2.HTM
,Как найти склон
Вот как найти склон. В уроке мы увидели, что такое уклон. Этот уклон является мерой того, насколько крутой является линия, и крутизна линии может быть измерена по следующей формуле: 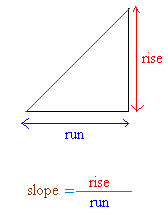 |
Как найти склон, когда подъем и трасса известны
Давайте проиллюстрируем это на нескольких примерах: 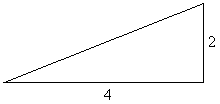 |
Для этой ситуации мы видим, что подъем равен 2, а пробег равен 4, поэтому наклон = 2/4
наклон = 1/2 после упрощения.
что означает 1/2?
Так как 1/2 положительно, вы идете в гору. Теперь предположим, что это подразделение во дворе.
1 — рост, 2 — бег. Это означает, что каждый раз, когда вы поднимаетесь на 1 ярд, вы проходите горизонтально или на 2 ярда.
Эта ситуация не очень крутая. Тем не менее, обратите внимание на следующее:
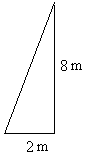 |
Здесь высота подъема составляет 8, а расстояние пробега или по горизонтали составляет 2
. Таким образом, наклон = 8/2 = 4 метра.
4 метра = 4/1 метра. Это означает, что каждый раз, когда вы поднимаетесь на 4 метра вверх, вы идете только на 1 метр по горизонтали.
Эта ситуация очень крутая, потому что вы поднимаетесь намного больше, чем горизонтально.
Как найти склон, когда мы не знаем подъем и бег.
Если мы построим график наклона в системе координат, мы сможем получить другую полезную формулу.Давайте тогда попробуем поместить наклон 4, как в предыдущем примере, в систему координат.
Поставь рост 8 куда угодно. Затем поставьте 2 балла. Вот и все!
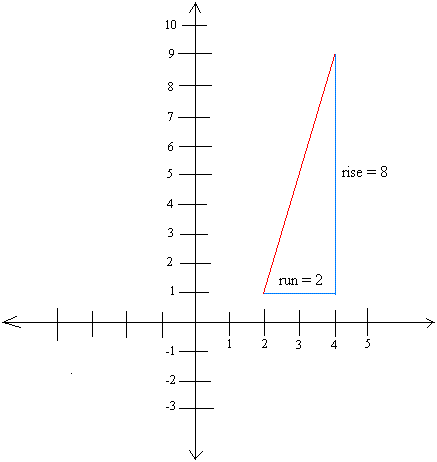
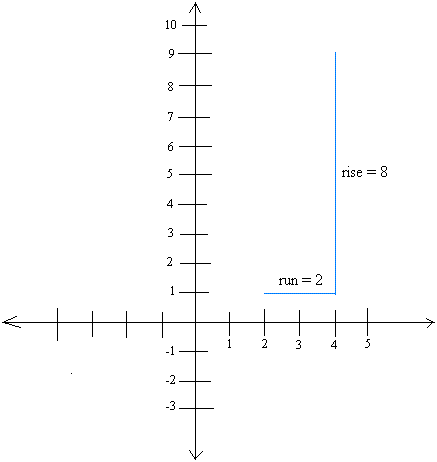 |
 |
Затем пометьте две конечные точки соответствующими координатами.
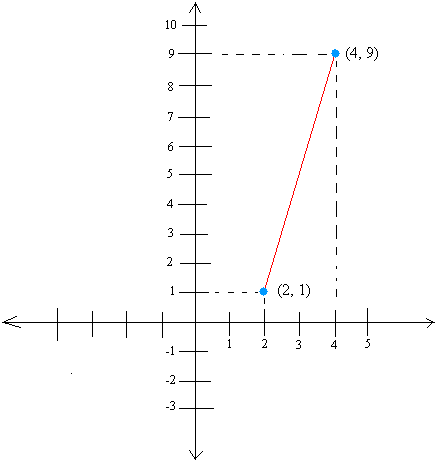 |
Обратите внимание, что 9 — 1 = 8 и 9 и 1 представляют собой y-координаты.
Поскольку мы не можем назвать обе координаты y, мы можем назвать одну y 1 , а другую y 2
Пусть y 1 = 9
Пусть y 2 = 1
Следовательно, 9 — 1 = y 1 — y 2 = 8 = рост
Также обратите внимание, что 4 — 2 = 2 и 4 и 2 представляют собой x-координаты.
Поскольку мы не можем назвать обе координаты x, мы можем назвать одну x 1 и назвать другую x 2
Позвольте x 1 = 4
Пусть x 2 = 2
Следовательно, 4 — 2 = x 1 — x 2 = 2 = пробег
Мы можем видеть, что
y 1 — y 2 = подъем и
x 1 — x 2 = пробег
Формула становится:
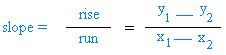 |
Итак, если подъем и бег не даны, но вы знаете по крайней мере две точки, используйте формулу справа выше.
Примеры: Как найти уклон при заданных точках.
1) (8, 8) и (4, 4)
Let (x 1 , y 1 ) = (8, 8) и (x 2 , y 2 ) = ( 4, 4)
(y 1 — y 2 ) / (x 1 — x 2 ) = (8 — 4) / (8 — 4) = 4/4 = 1
Поскольку 1 положительное, линия перемещается вверх при перемещении слева направо
2) (1, -5) и (2, -10)
Позвольте (x 1 , y 1 ) = ( 1, -5) и (x 2 , y 2 ) = (2, -10)
(y 1 — y 2 ) / (x 1 — x 2 ) = (-5 — -10) / (1 — 2) = (-5 + + 10) / — 1 = 5 / -1 = -5
Так как -5 отрицательно, линия уменьшается при перемещении слева направо
Обратите внимание, что
(y 2 — y 1 ) / (x 2 — x 1 ) = (-10 — -5) / (2 — 1) = (-10 + + 5) / 1 = -5/1 = -5
В целом уклон = (y 1 — y 2 ) / (x 1 — x 2 ) = (y 2 — y 1 ) / (x 2 — x 1 )
Теперь вам больше не интересно узнать, как найти склон !
Как найти викторину на склоне.Узнайте, насколько хорошо вы понимаете этот урок.
Новые уроки математики
Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.
,- Размер лдсп 16 мм эггер: ЛДСП 16х2800х2070 мм Egger. Декоры и цены | ООО «Строй-Провайдер»
- Дистанционное снятие показаний счетчиков электроэнергии ску – Дистанционный сбор показаний со счетчиков электроэнергии
