Сколько будет 6 в степени 3: Шесть в третьей степени — решение и ответ!

https://uchim.org/matematika/tablica-stepenej — uchim.org

Таблица степеней

Пример: 23=8 Степень: Число 2 3 4 5 6 7 8 9 10 2 4 8 16 32 64 128 256 512 1 024 3 9 27 81 243 729 2 187 6 561 19 683 59 049 4 16 64 256 1 024 4 096 16 384 65 536 262 144 1 048 576 5 25 125 625 3 125 15 625 78 125 390 625 1 953 125 9 765 625 6 36 216 1 296 7 776 46 656 279 936 1 679 616 10 077 696 60 466 176 7 49 343 2 401 16 807 117 649 823 543 5 764 801 40 353 607 282 475 249 8 64 512 4 096 32 768 262 144 2 097 152 16 777 216 134 217 728 1 073 741 824 9 81 729 6 561 59 049 531 441 4 782 969 43 046 721 387 420 489 3 486 784 401 10 100 1 000 10 000 100 000 1 000 000 10 000 000 100 000 000 1 000 000 000 10 000 000 000 11 121 1 331 14 641 161 051 1 771 561 19 487 171 214 358 881 2 357 947 691 25 937 424 601 12 144 1 728 20 736 248 832 2 985 984 35 831 808 429 981 696 5 159 780 352 61 917 364 224 13 169 2 197 28 561 371 293 4 826 809 62 748 517 815 730 721 10 604 499 373 137 858 491 849 14 196 2 744 38 416 537 824 7 529 536 105 413 504 1 475 789 056 20 661 046 784 289 254 654 976 15 225 3 375 50 625 759 375 11 390 625 170 859 375 2 562 890 625 38 443 359 375 576 650 390 625 16 256 4 096 65 536 1 048 576 16 777 216 268 435 456 4 294 967 296 68 719 476 736 1 099 511 627 776 17 289 4 913 83 521 1 419 857 24 137 569 410 338 673 6 975 757 441 118 587 876 497 2 015 993 900 449 18 324 5 832 104 976 1 889 568 34 012 224 612 220 032 11 019 960 576 198 359 290 368 3 570 467 226 624 19 361 6 859 130 321 2 476 099 47 045 881 893 871 739 16 983 563 041 322 687 697 779 6 131 066 257 801 20 400 8 000 160 000 3 200 000 64 000 000 1 280 000 000 25 600 000 000 512 000 000 000 10 240 000 000 000 21 441 9 261 194 481 4 084 101 85 766 121 1 801 088 541 37 822 859 361 794 280 046 581 16 679 880 978 201 22 484 10 648 234 256 5 153 632 113 379 904 2 494 357 888 54 875 873 536 1 207 269 217 792 26 559 922 791 424 23 529 12 167 279 841 6 436 343 148 035 889 3 404 825 447 78 310 985 281 1 801 152 661 463 41 426 511 213 649 24 576 13 824 331 776 7 962 624 191 102 976 4 586 471 424 110 075 314 176 2 641 807 540 224 63 403 380 965 376 25 625 15 625 390 625 9 765 625 244 140 625 6 103 515 625 152 587 890 625 3 814 697 265 625 95 367 431 640 625

Свойства степени — 2 части

Таблица основных степеней по алгебре в компактном виде (картинка, удобно, чтобы распечатать), сверху числа, сбоку степени:

(можно открыть в новом окне, нажав на картинку)

Полную математическую таблицу можно бесплатно скачать, просто сохранив картинку выше с помощью правой кнопки мыши.

Всё для учебы » Математика в школе » Таблица степеней по алгебре

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Ссылка: https://uchim.org/matematika/tablica-stepenej

Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней

Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности, геометрии и математике! Также на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!

Степень

Результат:

n	1	2	3	4	5	6	7	8	9	10
1n	1	1	1	1	1	1	1	1	1	1
2n	2	4	8	16	32	64	128	256	512	1024
3n	3	9	27	81	243	729	2187	6561	19683	59049
4n	4	16	64	256	1024	4096	16384	65536	262144	1048576
5n	5	25	125	625	3125	15625	78125	390625	1953125	9765625
6n	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7n	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8n	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9n	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10n	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

---

Таблица степеней от 1 до 10

11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1	21=2 22=4 23=8 24=16 25=32 26=64 27=128 28 =256 29=512 210=1024	31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049	41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576	51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176	71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249	81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824	91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910 =3486784401	101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000

Остались вопросы?

Здесь вы найдете ответы. x=3 log2(3)=x

90 в 10 степени

90 в 10 =34867844009999998976.00000

12 в степени 1/3

Сложная формула но в кратце ответ — 6

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Чему равно 6 в 3-й степени?

Улучшить статью

Сохранить статью

Нравится Статья

• Последнее обновление: 21 сен, 2021

Читать

Обсудить

Улучшить статью

Сохранить статью

Нравится Статья

Экспоненты и степени — это метод многократного умножения одного и того же числа. Например, 7×7×7 можно записать как 7 ³ , где 7 — основание, а 3 — показатель степени. Чаще всего он используется для выражения степени 10, чтобы записать очень большое число в удобной форме. Например, 1000 можно записать как 10 ³ .

Законы экспоненты

• Чтобы умножить два экспоненциальных числа с одинаковыми основаниями, степени складываются, а основание остается прежним.
  Например, a ^m × a ⁿ = a ^m+n .
• Когда показатель степени имеет другой показатель степени, основание остается прежним, но степени умножаются.
  Например, (a ^m ) ⁿ = a ^m×n .
• Чтобы разделить два экспоненциальных числа с одинаковыми основаниями, степени вычитаются, а основание остается прежним.
  Например, a ^m / a ⁿ = a ^m-n .

Что такое степенная запись?

Представление в степени — это метод выражения очень больших или очень маленьких чисел. Например, 1000000000000 можно записать как 10 ¹² , а 0,00000026 можно записать как 2,6 × 10 ^-7 .

Шаги для вычисления значения экспоненциального числа:

• Запишите число с его показателем степени.
• Умножьте число на себя на количество раз, равное его мощности.
• Убедитесь, что расчет правильный.

Что такое 6-я в 3-й степени?

Решение:

Учитывая, что число равно 6, а степень равна 3.

Запишите число с его показателем степени.

6 ³ = 6 × 6 × 6

6 ³ = 216

Следовательно, значение от 6 до 3 -й мощности — 216.

Аналогичные вопросы

Вопрос 1: Что является 12 -м. в 4 степени?

Решение:

Учитывая, что число равно 12, а степень равна 4.

Запишите число с его показателем степени.

12 ⁴ = 12 × 12 × 12 × 12

12 ⁴ = 20736

Следовательно, значение от 12 до 4 -го мощности — 20736.

Вопрос 2: 3rd 6-я сила?

Решение:

Учитывая, что число равно 3, а степень равна 6.

Запишите число с показателем степени.

3 ⁶ = 3 × 3 × 3 × 3 × 3 × 3

3 ⁶ = 729

Следовательно, число 3 в шестой степени равно 729.

2 Вопрос 15-е в 3-й степени?

Решение:

Учитывая, что число равно 15, а степень равна 3.

Запишите число с показателем степени.

15 ³ = 15 × 15 × 15

15 ³ = 3375

Следовательно, число 15 в 3-й степени равно 3375.

Нравится статья

Сохранить статью

Калькулятор экспоненты

Создано Матеушем Мухой и Петром Малеком

Отредактировано Богной Шик и Джеком Боватером

Последнее обновление: 12 февраля 2023 г.

Содержание:

• Что такое экспонента?
• Калькулятор отрицательного показателя степени
• Похожие темы
• Часто задаваемые вопросы

Калькулятор степени вычисляет значение любого основания, возведенного в любую степень. На этой странице будут рассмотрены все связанные темы, включая отрицательную экспоненту. Начнем с основ.

Что такое экспонента?

Показатель степени — это способ представить, сколько раз число, известное как основание, умножается само на себя. Он представлен в виде небольшого числа в правом верхнем углу базы. Например: x² означает, что вы умножаете x на себя два раза, что равно x × x . Аналогично, 4² = 4 × 4 и т. д. Если показатель степени равен 3, в примере 5³ , тогда результат будет 5 × 5 × 5 .

Это просто с небольшими числами, но для больших чисел, десятичных дробей или когда они возведены в очень большую или отрицательную степень, используйте наш инструмент. Если вы хотите возвести в степень вручную, сделайте следующее:

1. Определите основание и степень, в которую оно возведено, например, 3⁵ .
2. Запишите основание столько же раз, сколько и показатель степени. 3 3 3 3 3
3. Поместите символ умножения между каждым основанием. 3 × 3 × 3 × 3 × 3 .
4. Умножай! 3 × 3 × 3 × 3 × 3 = 243 .

Калькулятор отрицательного показателя степени

Концепция довольно проста, когда показатель степени положительный, но что происходит, когда показатель степени отрицательный? По определению, если оно равно -2, мы должны умножить само основание на 9.0242 минус два раза. На самом деле то, что здесь происходит, мы берем обратное основание, меняем отрицательный показатель степени на положительный и действуем как обычно. Если вы хотите решить это вручную, сделайте следующее:

1. Определите основание и показатель степени.
2. Напишите обратную величину основания и измените знак экспоненты на положительный
3. Запишите обратное основание столько же раз, сколько и показатель степени.
4. Поместите между каждым символ умножения.
5. Умножь и получи результат.

Вот простой пример: 5⁻⁴ = (1/5)⁴ = (1/5) × (1/5) × (1/5) × (1/5) = 1/625 = 0,0016

Возведение в квадрат основания (возведение числа в степень 2) и извлечение квадратного корня — схожие понятия; многие люди считают одно противоположным или уничтожающим другое. Если вы хотите возвести в квадрат число 6, возьмите 6 × 6 = 36 . Теперь, если вы хотите найти, при умножении двух одинаковых чисел получается 36, вы берете квадратный корень из 36. Этот квадратный корень дает значение 6. Можно также отметить, что возведение квадратного корня в квадрат удаляет радикал.

Аналогичным образом, возведение основания в куб (возведение числа в степень 3) даст нам идеальный куб. Если вам нужно вычислить кубический корень, вы можете воспользоваться нашим калькулятором кубического корня, который является отличным инструментом для вычисления кубического корня любого числа.

В модульной арифметике существуют специальные методы возведения в степень — узнайте больше с помощью калькулятора модуля мощности.

Кроме того, вы можете воспользоваться нашим калькулятором логарифмов, который является обратной функцией показателя степени.

Любое число, возведенное в степень 0, равно 1. Калькулятор отрицательного показателя степени полезен при работе с экспоненциальным затуханием, формула которого имеет отрицательный показатель степени.

Часто задаваемые вопросы

Что такое 6 с показателем степени 4?

1296 . Чтобы вычислить 6 с показателем степени 4 , запишите его как 6 ⁴ и умножьте четыре экземпляра 6 вместе. Его можно записать как 6 × 6 × 6 × 6 = 1296 .

Как умножить показатели степени?

Если вы хотите умножить на степени , убедитесь , что они имеют одинаковое основание . Затем просто добавьте исходные показатели степени , чтобы найти новую степень произведения. Например, чтобы получить , умножьте 2 ³ на 2 ⁵ :

1. Добавьте 3 + 5 = 8 .
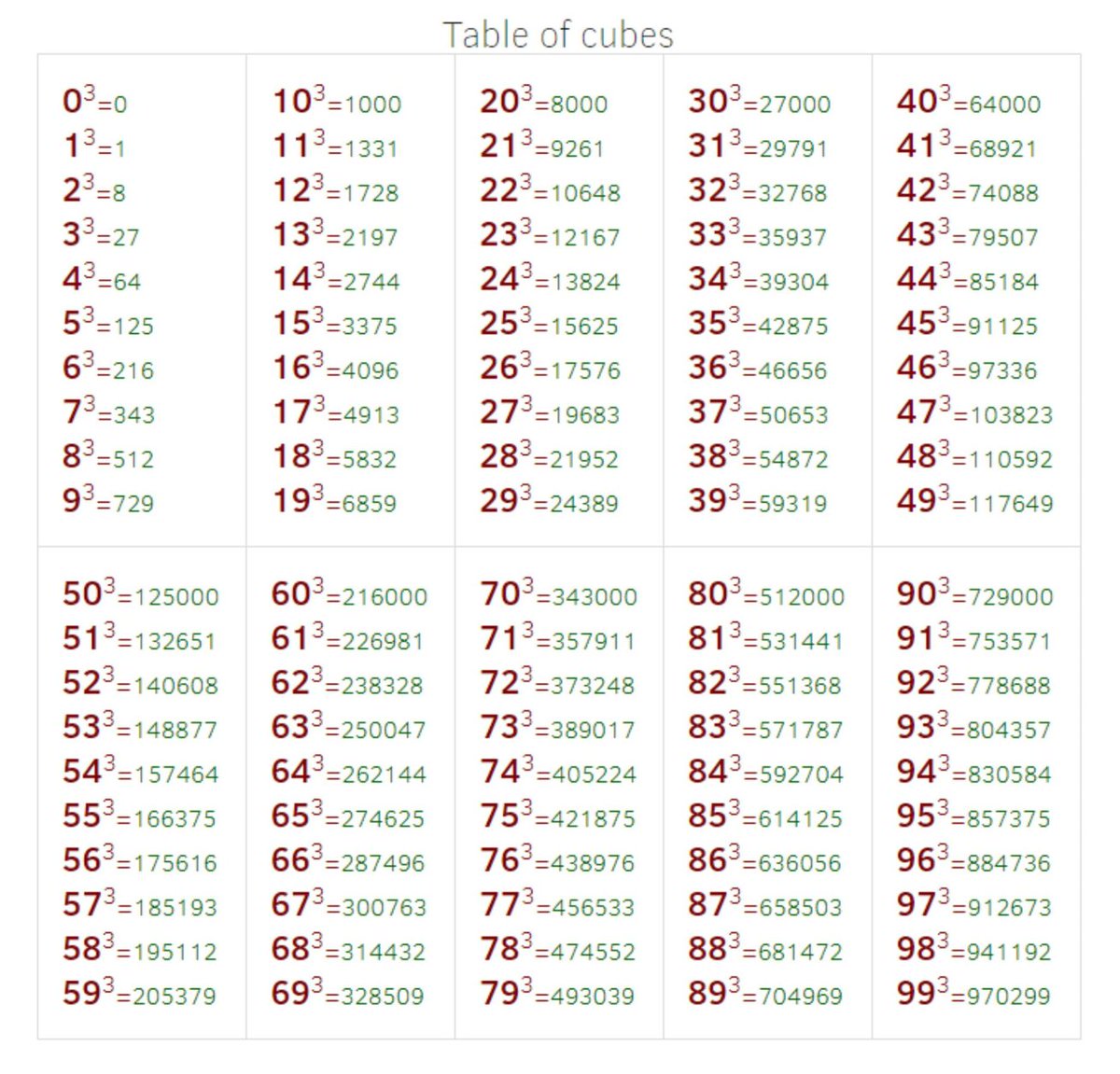
   Сколько будет 6 в степени 3: Шесть в третьей степени — решение и ответ!