ᐉ Расчет пиломатериала • Таблица, кулькулятор, примеры
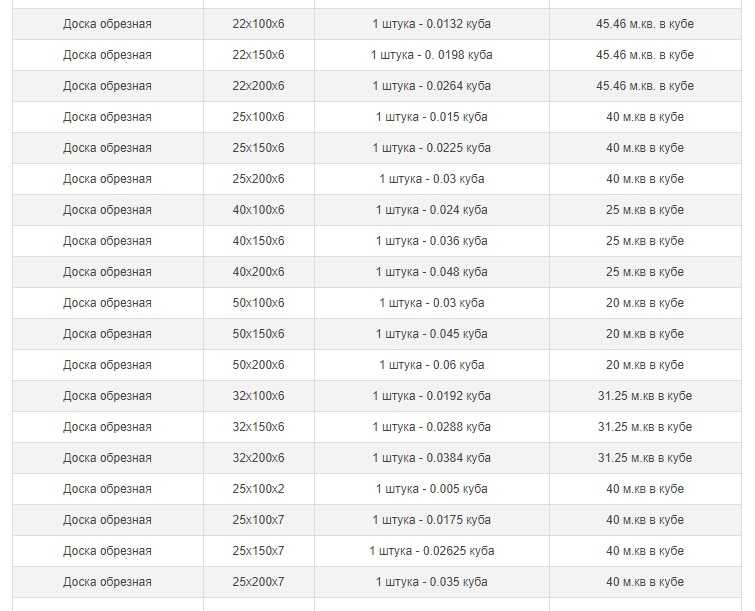
Для упрощения счета, мы подготовили для Вас сводную таблицу. Таблица позволяет сразу узнать, сколько досок в 1 кубе, количество погонных метров в 1 кубе, объем 1 доски и площадь 1 доски, не уделяя время лишним расчетам.
Формулы расчета доски
Кубатура
Примеры расчета доски размером 25х100х4000 мм
Формула расчета объема 1 доски:
0,025 м · 0,1 м · 4 м = 0,01 м3
Формула расчета количества досок в 1 кубе:
1 м3 / 0,01 м3 = 100 шт./м3
Квадратура
Примеры расчета доски размером 25х100х4000 мм
Формула расчета квадратуры 1 доски:
0,1 м · 4 м = 0,4 м2
Формула расчета количества квадратов в 1 кубе:
100 шт.(количество досок в кубе) · 0,4 м = 40 м2/ в 1 м3
Чтобы решить, сколько досок в 1 кубе, сначала нужно знать основные параметры приобретаемого материала – толщину, ширину и длину.
Также можно делать расчет для досок любого сечения и длины.
Обрезная доска 25мм, 4000мм
| Обрезная доска, 25мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 1 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 25х100х4000 | 0,01 м3 | 100 шт. | 400 метров. | 0,4 м2 |
| 25х120х4000 | 0,012 м3 | 83,3 шт. | 333,2 метра. | 0,48 м2 |
| 25х150х4000 | 0,015 м3 | 66,6 шт. | 266,4 метра. | 0,6 м2 |
| 25х200х4000 | 0,02 м3 | 50 шт. | 200 метров. | 0,8 м2 |
Обрезная доска 25мм, 4500мм
| Обрезная доска, 25мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 1 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 25х100х4500 | 0,01125 м3 | 88,8 шт. | 399,6 метра. | 0,45 м2 |
| 25х120х4500 | 0,0135 м3 | 74 шт. | 333 метра. | 0,54 м2 |
| 25х150х4500 | 0,0169 м3 | 59,2 шт. | 266,4 метра. | 0,675 м2 |
| 25х200х4500 | 0,0225 м3 | 44,4 шт. | 199,8 метров. | 0,9 м2 |
Обрезная доска 30мм, 4000мм
| Обрезная доска, 30мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 2 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 30х100х4000 | 0,012 м3 | 83,3 шт. | 333,2 метра. | 0,4 м2 |
| 30х120х4000 | 0,0144 м3 | 69,4 шт. | 277,6 метра. | 0,48 м2 |
| 30х150х4000 | 0,018 м3 | 55,5 шт. | 222 метра. | 0,6 м2 |
| 30х200х4000 | 0,024 м3 | 41,6 шт. | 166,4 метра. | 0,8 м2 |
Обрезная доска 30мм, 4500мм
| Обрезная доска, 30мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 1 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 30х100х4500 | 0,0135 м3 | 74 шт.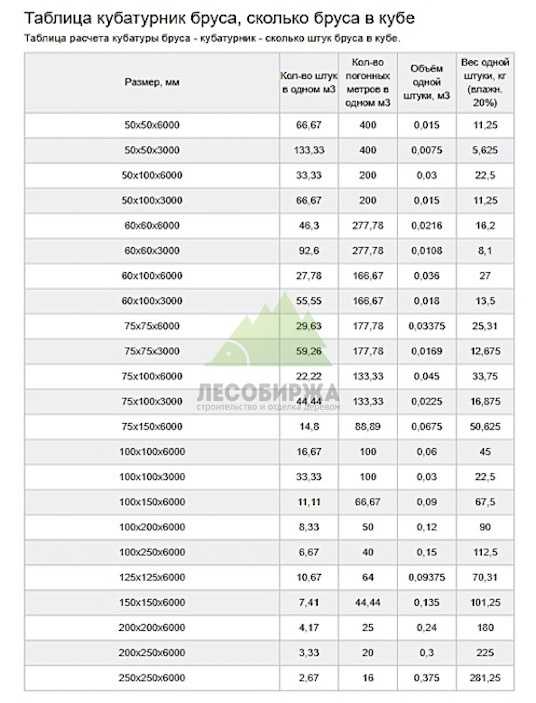 | 333 метра. | 0,45 м2 |
| 30х120х4500 | 0,0162 м3 | 61,7 шт. | 377,65 метра. | 0,54 м2 |
| 30х150х4500 | 0,0203 м3 | 49,3 шт. | 221,85 метра. | 0,675 м2 |
| 30х200х4500 | 0,027 м3 | 37 шт. | 166,5 метра. | 0,9 м2 |
Страница содержит ответы на частые вопросы клиентов:
- Сколько досок
- Сколько кубов доски
- Сколько штук досок
- Досок в кубе
- Сколько кубов в досках
- Сколько штук в одном кубе
- Сколько в кубе обрезной доски
- Как подсчитать сколько досок в 1 кубе
- Количество досок в кубе
- Сколько квадратов в кубе
Зачем считать, сколько досок в 1 кубе?
Всего две причины для того, чтобы произвести расчеты:
- Вы узнаете общую цену всего объема бруса, нужного для вашего проекта. Достаточно знать цену за 1 доску и сколько всего штук (определяется расчетным путем или из нашей таблицы для стандартных размеров досок).
- Вы подсчитаете общее число досок, нужное для осуществления вашего проекта. И сделать расчет можно, зная, сколько нужно кубов материала для работы, и определив количество штук досок в 1 кубе.
Но если боитесь сделать неправильные расчеты, Вы всегда можете позвонить по нашим телефонам и наши специалисты помогут разобраться с правильным подсчетом!
Сколько в кубе доски 25х100х6000? -Полезные советы
Что такое куб доски?
По стандартам для измерения пиломатериалов принята такая мера как куб. Чаще всего есть необходимость рассчитать количество досок в одном кубе стройматериала определенного вида.
Существует несколько способов для расчётов:
- Воспользоваться готовыми таблицами (если доска идет стандартной ширины и длины)
- Воспользоваться калькулятором для расчета
- Рассчитать по формуле — способ подходит для любого вида пиломатериалов с любыми размерами, в том числе нестандартными
Расчет количества досок в кубометре по формуле
Для расчета нам необходимо знать следующие параметры доски:
- Толщина
- Длина
- Ширина
Все измерения проводятся в метрах.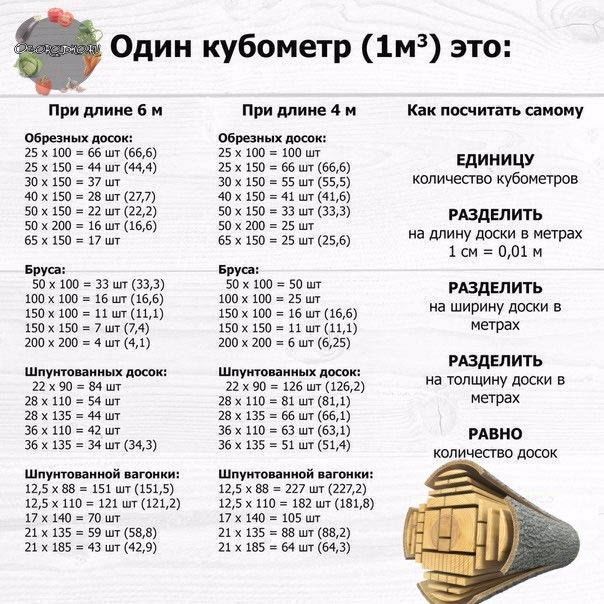
Формула для расчета количества досок в кубометре:
Количество досок в кубометре = 1/(Длина доски Х Ширина Доски Х Толщина)
Измерения округляем до целого числа в большую сторону.
Для примера возьмем доску длиной 6000мм (переводим в метры – 6м), ширина 100 мм (или 0,1метра), толщина 25 мм (0,025м):
Количество досок = 1/ (6х0,1х0,025) = 66,7
Результат: в кубе доски 25х100х6000 находится 67 штук.
Калькулятор для расчета обычно работает по тому же принципу, что и формула, в него необходимо внести эти же данные.
Готовые справочки по расчету количества доски в кубометрах
В готовых справочниках предоставляется информация для стандартных размеров доски:
— толщина от 20 до 50мм
— длина – от 1 до 6 метров
— ширина – от 10 до 25 см
В справочниках есть информация для различных видов пиломатериалов – от обрезной доски до бруса.
При таких запросах как: Сколько 40 доски в кубе? Нужно понимать, что количество зависит не только от толщины («сороковка» или 40мм толщины), но и от длины и ширины доски.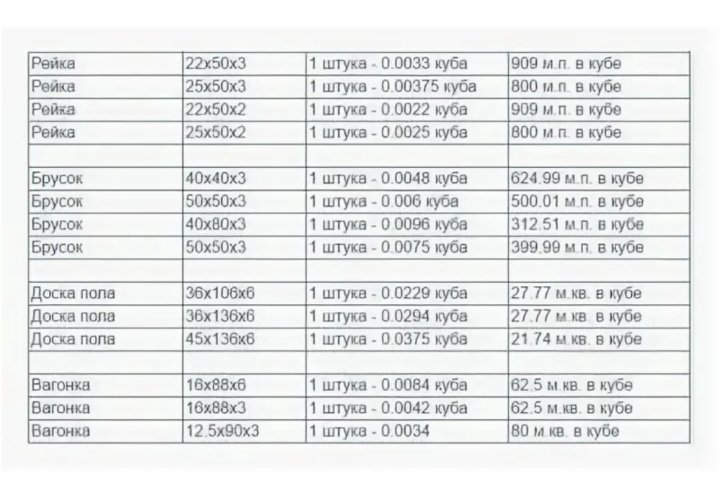
Сколько доски в кубе – самые часто используемые размеры
Доска 50х150х600 (или шестиметровая доска 50х150) — 23 доски.
Доска 150х40х6000 сколько штук в кубе – 28 досок.
Доска обрезная 25х150х6000 сколько досок в кубе – 45 штук.
Сколько в кубе доски 25х100х6000 – 67 досок.
Как рассчитать количество досок необходимое для покрытия определенной площади?
Этот параметр рассчитывается умножением длины и ширины доски. Все данные указываются в метрах.
Если для примера берем доску: 25х100х6000 – для расчета покрытия показатель толщины доски нам не важен: 0,1м х 6 = 0,6 кв. м – покрывает одна доска. Как ранее мы сосчитали, что в кубе 67 досок, то получается из куба доски мы покроем:
67*0,6= 40,2 квадратных метра будет покрыто 1 кубометром доски.
Стоит учесть, что площадь покрытия считается исходя из поверхности доски без монтажных пазов, если они есть, например на евровагонке.
Остались вопросы?
Подобрать материал необходимого качества и проконсультировать по размерам, монтажу и обработке могут наши консультанты.
Наши контакты
Заказать звонок или позвоните по номеру +7(951)061-80-42, +7(843)216-49-36 или отправляйте ваш запрос на почту
Обращайтесь!
Возможно Вам будет интересно!
Баня из бруса Все полезные советы Сколько весит куб сосны? Покупайте доску у нас:
Сколько клеток на шахматной доске?
Сколько клеток на шахматной доске? В зависимости от вашей интерпретации, это может быть воспринято как вопрос с подвохом. Ответ 64 квадрата (8×8) совершенно верен, но есть и альтернативный ответ, если мы посчитаем квадраты разных размеров, а не только отдельные квадраты.
Например, есть один квадрат размером 8×8 единиц:
Тогда есть четыре квадрата размером 7×7 единиц:
И девять квадратов размером 6×6 единиц:
Я уверен, что вы уже видели узор. По мере того, как мы постепенно уменьшаем целевой квадрат на одну единицу, мы можем найти идеальный квадрат несколько раз.
Имеется 2×2 начальных позиций, с которых может начинаться (7×7) клеток, имеется 3×3 начальных позиций, с которых может начинаться (6×6) клеток …
Общее количество квадраты таким образом:
Существует также формула для быстрого вычисления суммы квадратов. Для шахматной доски с n=8 мы видим, что сумма равна 204.
Интересно, что по мере увеличения n эта формула стремится к n 3 /3 . Я уверен, что из этого есть какие-то особенно крутые последствия, но я не могу придумать ни одного в данный момент. Если вы думаете об одном, напишите мне, и я обновлю эту страницу и отдам вам должное!
Обновление!
Изображение: Изабель призывает к миру всех студентов-историков Кредит: Рэйчел
Я получил приятное электронное письмо от Маноса Камарианакиса, который предложил следующее:
«Следствие суммы n 2 , стремящейся к n 3 /3.
Нашла в интернете картинку такого зиккурата, сделанного из кубиков сахара!
Прямоугольники
Как насчет количества прямоугольников на шахматной доске? Что ж, чтобы сделать прямоугольник, вам нужно выбрать любые две вертикальные линии и любые две горизонтальные линии. Есть 9 C 2 пары горизонтальных линий, которые вы можете выбрать (36 различных пар), и столько же вертикальных пар, поэтому ответ 36 × 36 = 1296.
Вот таблица первых нескольких квадратных сеток и количество квадратов и прямоугольников:
| Board Size | # Squares | # Rectangles |
|---|---|---|
| 1×1 | 1 | 1 |
| 2×2 | 5 | 9 |
| 3×3 | 14 | 36 |
| 4×4 | 30 | 100 |
| 5×5 | 55 | 225 |
| 6×6 | 91 | 441 |
| 7×7 | 140 | 784 |
| 8×8 | 204 | 1,296 |
| 9×9 | 285 | 2,025 |
| 10×10 | 385 | 3,025 |
Реклама:
2002 Головоломка
Все началось с того, что я наткнулся на старую головоломку, созданную, приписываемую Эриху Фридману, в 2002 году:
Возьмите сетку из 18×18 квадратов и удалите два из них так, чтобы полученная фигура содержала ровно 2002 квадрата всех размеров, составленных из оставшихся квадратов.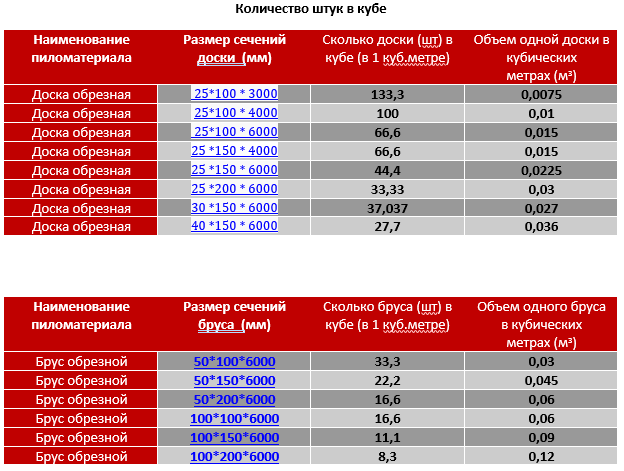
В Интернете есть ответ, но я не мог с ним согласиться, поэтому написал немного кода, чтобы сгенерировать все ответы.
Если вы хотите попробовать сами, вот апплет ниже. В этом варианте вы также можете указать различные размеры сетки и количество заштрихованных блоков, которые вам разрешено устанавливать.
Решения
Вы нашли решение? Если вы хотите увидеть все 64 решения (, а не , дедублированные поворотами или отражениями), нажмите ниже.
1.2 Комбинации и перестановки
Сначала обратимся к , считая . Хотя это звучит просто, возможно, слишком
просто учиться, это не так. Когда мы говорим о счете, это стенография
для определения размера множества или, чаще, размеров многих
наборы, все с чем-то общим, но разные размеры в зависимости от
один или несколько параметров. Например: сколько исходов возможно
когда бросают кубик? Две кости? $n$ кости? Как сказано, это
двусмысленно: что мы подразумеваем под «результатом»? Предположим, мы бросаем две кости,
скажем, красный кубик и зеленый кубик.
Даже довольно простая первая интерпретация опирается на некоторую степень
знание счета; мы сначала выясним два простых факта. В
с точки зрения размеров множества, предположим, что мы знаем, что множество $A$ имеет размер $m$ и множество
$B$ имеет размер $n$. Каков размер $A$ и $B$ вместе, то есть
размер $A\cup B$? Если мы знаем, что $A$ и $B$ не имеют элементов в
общий, то размер $A\cup B$ равен $m+n$; если у них есть элементы в
общее, нам нужно больше информации. Простая, но типичная проблема этого
тип: если мы бросим два кубика, сколько существует способов получить либо 7, либо
11? Так как есть 6 способов получить 7 и два способа получить 11,
ответ: $6+2=8$. Хотя этот принцип прост, его легко
забыть требование непересекаемости двух множеств и, следовательно, использовать
это когда обстоятельства иные.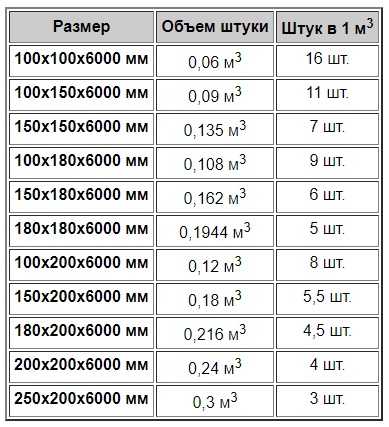
Почему мы знаем, не перечисляя их всех, что существует 36 исходов?
когда бросают две игральные кости? Мы можем рассматривать результаты как два отдельных
результаты, то есть результат броска кубика номер один и
результат броска кубика номер два. По каждому из 6 исходов
первый кубик второй кубик может иметь любой из 6 исходов, поэтому сумма равна
$6+6+6+6+6+6=36$ или, более компактно, $6\cdot6=36$. Обратите внимание, что мы
здесь действительно используется принцип сложения: set $A_1$ — это все пары
$(1,x)$, набор $A_2$ — это все пары $(2,x)$ и т. д. это несколько
более тонким, чем кажется на первый взгляд. В этом простом примере
результаты кубика номер два не имеют ничего общего с результатами кубика
номер один. Вот немного более сложный пример: сколько способов
можно ли бросить два кубика так, чтобы два кубика не совпали? То есть,
исключаем 1-1, 2-2 и так далее. Здесь для каждого возможного значения на кубике
число один, есть пять возможных значений кубика номер два, но
это разные пять значений для каждого значения на номере кубика
один.
Пример 1.2.1 Сколько исходов возможно при броске трех игральных костей, если не может быть двух одинаковых? Первые две кости вместе имеют $6\cdot 5=30$ возможных исходов, сверху. Для каждого из этих 30 исходов, есть четыре возможных исхода для третьего кубика, поэтому общее количество исходов $30\cdot 4=6\cdot 5\cdot 4=120$. (Обратите внимание, что мы считаем кости различимыми, то есть броском 6, 4, 1 отличается от 4, 6, 1, потому что первое и второе кости различны в двух бросках, даже несмотря на то, что числа как набор одинаковы.) $\квадрат$
Пример 1.2.2. Предположим, что блоки с номерами от 1 до $n$ находятся в бочке; мы
вытащите из них $k$, расположив их в линию, как мы.
Сколько
исходы возможны? То есть, сколько различных расположений $k$
блоки могли бы мы видеть?
По сути, это то же самое, что и в предыдущем примере: имеется $k$ «пятен». заполняться блоками. Любой из блоков $n$ может появиться первым в линия; то любой из оставшихся $n-1$ может появиться следующим, и, таким образом, на. Таким образом, число исходов равно $n(n-1)(n-2)\cdots(n-k+1)$, согласно принцип умножения. в В предыдущем примере первое «пятно» было номером один, второе точка была номером два, третья точка была номером три, и $6\cdot5\cdot4=6(6-1)(6-2)$; обратите внимание, что $6-2=6-3+1$. $\квадрат$
Это довольно общая проблема:
Определение 1.2.3 Количество перестановок $n$ вещи, взятые $k$ за раз, $$P(n,k)=n(n-1)(n-2)\cdots(n-k+1)={n!\over (n-k)!}.$$ $\квадрат$
Перестановка некоторых объектов представляет собой конкретное линейное упорядочение
объекты; Фактически $P(n,k)$ одновременно учитывает две вещи:
количество способов выбрать и упорядочить $k$ из $n$ объектов.
Предположим, мы хотим подсчитать только количество способов выбрать $k$ предметов. из $n$, то есть порядок нам не важен. В Пример 1.2.1, мы подсчитали количество броски трех игральных костей с разными числами. Кости были различимы или в определенном порядке: первый кубик, второй и третий. Теперь мы хотим просто посчитать, сколько комбинаций чисел есть, причем 6, 4, 1 теперь считаются той же комбинацией, что и 4, 6, 1.
Пример 1.2.4
Предположим, нам нужно перечислить все 120 возможностей в
пример 1.2.1. Список будет содержать
множество исходов, которые мы теперь хотим считать одним исходом;
6, 4, 1 и 4, 6, 1 будут в списке, но не должны учитываться
в отдельности.
Следуя тем же рассуждениям вообще, если у нас есть $n$ объектов, количество способов выбрать $k$ из них $P(n,k)/k!$, так как каждый набор из $k$ объектов будет посчитал $k!$ раз по $P(n,k)$.
Определение 1.2.5 Количество подмножеств размера $k$ множества размера $n$ (также называется $n$-множеством) $$C(n,k)={P(n,k)\более k!}={n!\over k!(n-k)!}={n\выбрать k}.$$ Обозначение $C(n,k)$ используется редко; вместо этого мы используем $n\выбрать k$, произносится как «$n$ выбирает $k$». $\квадрат$
Пример 1.2.6
Рассмотрим $n=0,1,2,3$. Несложно перечислить
подмножества малого $n$-множества; типичное $n$-множество
$\{a_1,a_2,\ldots,a_n\}$.
$0$-множество, а именно пустое множество, имеет
одно подмножество, пустой набор; $1$-множество имеет два подмножества, пустое множество
и $\{a_1\}$; $2$-подмножество имеет четыре подмножества, $\emptyset$, $\{a_1\}$,
$\{a_2\}$, $\{a_1,a_2\}$; а $3$-подмножество имеет восемь:
$\emptyset$, $\{a_1\}$, $\{a_2\}$, $\{a_3\}$, $\{a_1,a_2\}$,
$\{a_1,a_3\}$, $\{a_2,a_3\}$, $\{a_1,a_2,a_3\}$.
Затем из этих списков легко вычислить $n\выбрать k$:
$$\displaylines{\cr
\матрица{
&\rlap{\lower 3pt\hbox{$\Rule{65pt}{0pt}{0.5pt}$}}\cr
&0\кр
п&1\кр
&2\кр
&3\кр
}\влево\верт
\матрица{
0&\нижний 3.5pt\hbox{}\rlap{\smash{\поднять 1.5em \hbox{$k$}}}1&2&3\cr
1\кр
1&1\кр
1&2&1\кр
1&3&3&1\кр
}\право.\cr}$$
$\квадрат$
Вы, наверное, узнаете эти цифры: это начало Треугольник Паскаля . Каждая запись в
Треугольник Паскаля получается путем добавления двух элементов из предыдущего
ряд: тот, что прямо сверху, и тот, что выше и левее. Этот
предполагает, что ${n\выбрать k}={n-1\выбрать k-1}+{n-1\выбрать k}$, и
действительно это правда.
Чтобы сделать это аккуратно, мы принимаем
соглашение о том, что ${n\choose k}=0$, когда $kn$.
Теорема 1.2.7 $\ds{n\выберите k}={n-1\выберите k-1}+{n-1\выберите k}$.
Доказательство. Типичным $n$-множеством является $A=\{a_1,\ldots,a_n\}$. Мы рассматриваем два типа подмножества: содержащие $a_n$ и не содержащие. Если $k$-подмножество $A$ не содержит $a_n$, то оно является $k$-подмножеством $\{a_1,…,a_{n-1}\}$, и таких $n-1\выберите k$. Если оно содержит $a_n$, то он состоит из $a_n$ и $k-1$ элементов $\{a_1,…,a_{n-1}\}$; так как их $n-1\выберите k-1$, таких подмножеств $n-1\выберите k-1$. Таким образом, общее количество $k$-подмножеств $A$ равно ${n-1\выбрать k-1}+{n-1\выбрать k}$.
Обратите внимание, что когда $k=0$, ${n-1\выберите k-1}={n-1\выберите -1}=0$, и когда $k=n$, ${n-1\выбрать k}={n-1\выбрать n}=0$, так что ${n\выбрать 0}={n-1\выбрать 0}$ и ${n\выбрать n}={n-1\выбрать п-1}$. Эти значения являются граничными в треугольнике Паскаля. $\qed$
Многие проблемы со счетом основаны на рассуждениях, которые у нас есть.
видимый. Вот несколько вариаций на тему.
Пример 1.2.8 Шесть человек должны сидеть за круглым столом; сколько сидячих мест аранжировки есть?
Не совсем ясно, что именно мы имеем в виду, чтобы считать здесь. если есть «специальное место», например, может иметь значение, кто окажется на этом сиденье. Если это не имеет значения, нас интересует только относительное положение каждого человека. Тогда может или не может быть важно, является ли определенное лицо находится слева или справа от другого. Так что этот вопрос можно интерпретируется (по крайней мере) тремя способами. Давайте ответим на них все.
Во-первых, если имеют значение фактические стулья, на которых сидят люди, то это
точно так же, как выстраивание шести человек в ряд: 6 вариантов места
номер один, 5 для второго места и так далее, всего 6 долларов! Если
стулья не имеют значения, тогда $6!$ считают одно и то же расположение слишком большим
раз, по одному разу для каждого человека, который может быть на первом месте.
Итак, общее количество в
в этом случае $6!/6=5!$. Другой подход к этому: поскольку фактическое
места не имеют значения, просто посадите одного из шести человек на стул. Тогда мы
нужно расставить оставшихся 5 человек в ряд, что можно сделать в
$5!$ способов. Наконец, предположим, что нас волнует только то, кто рядом с кем,
игнорируя право и лево. Тогда предыдущий ответ считает каждый
расположение дважды, один раз для порядка против часовой стрелки и один раз для
по часовой стрелке. Итого $5!/2=P(5,3)$.
$\квадрат$
Мы дважды видели общий принцип в действии: если мы можем пересчитать желаемый набор таким образом, чтобы каждый элемент считался одинаковым количество раз, мы можем получить желаемое количество, просто разделив на общий фактор пересчета. Это по-прежнему будет полезной идеей. А вариация на эту тему состоит в том, чтобы пересчитать , а затем вычесть из сумма перерасчета.
Пример 1.2.9. Сколькими способами можно выстроить шесть человек так, чтобы конкретная пара людей не является соседней?
Обозначим людей $A$ и $B$.
Общее количество заказов составляет $6!$, но здесь учитываются заказы с
$A$ и $B$ рядом друг с другом. Сколько из них есть? Думать о
эти два человека как единое целое; сколько существует способов выстроить
Блок $AB$ с остальными четырьмя людьми? У нас есть 5 предметов, поэтому ответ
$5!$. Каждый из этих порядков соответствует двум различным порядкам в
которые $A$ и $B$ являются смежными, в зависимости от того, является ли $A$ или $B$
первый. Таким образом, количество $6!$ слишком велико на $2\cdot5!$ и количество, которое мы
seek равен $6!-2\cdot 5!=4\cdot5!$.
$\квадрат$
9{e_n}$ есть, где
$p_i$ — различные простые числа?
Пример 1.2.2 Покерная рука состоит из пяти карт из стандартных 52 карт. колода с четырьмя мастями и тринадцатью достоинствами в каждой масти; получатель чего-то карты в руке значения не имеют. Из скольких рук состоит 2 карты одного достоинства и 3 карты другого достоинства (фулл-хаус)? Сколько состоит из 5 карт одной масти (флеш)?
Пример 1.
2.3 Шестеро мужчин и шесть женщин должны сидеть за столом,
мужчины и женщины чередуются. Стулья не имеют значения, важно только, кто следующий
кому, а правое и левое разные. Сколько сидячих мест
аранжировки возможны?
Пример 1.2.4 Восемь человек должны сидеть за столом; стулья неважно, только кто рядом с кем, а справа и слева другой. Два человека, X и Y, не могут сидеть рядом друг с другом. Сколько посадочных мест возможно?
Пример 1.2.5 В шахматах ладья атакует любую фигуру в той же строке или столбце. как ладья, если между ними нет другой фигуры. Сколькими способами можно ли разместить на шахматной доске восемь неразличимых ладей так, чтобы двое не нападают друг на друга? Как насчет восьми неразличимых ладей на доска $10\times 10$?
Пример 1.2.6 Предположим, мы хотим поставить 8 неатакующих ладей на поле. шахматная доска. Сколькими способами мы можем это сделать, если 16 наиболее Квадраты «северо-запад» должны быть пустыми? А если только 4 самых Квадраты «северо-запад» должны быть пустыми?
Пример 1.