Расчет несущей способности и прогиба деревянных балок: Инструкции +Фото и Видео
Расчет несущей способности и прогиба деревянных балок. Для строительства деревянного дома потребуется провести расчет несущей способности деревянной балки. Не менее важное значение в терминологии строителей уделяется определению прогиба. Без хорошего математического анализа каждого из параметров невозможно выстроить красивый и надежный дом из бруса. Именно по этой причине перед началом строительства очень важно, чтобы был правильно рассчитан прогиб балок из дерева.
Такие расчеты будут залогом того, что ваша постройка будет надежной и качественной.
Что требуется для правильного расчета?
Расчет деревянной балки на прогиб и несущей способности не такая простая задача, как может показаться кому-то вначале. Чтобы понять, какое количество досок вам потребуется, а также, какого они должны быть размера, следует потратить много времени, или же просто использовать специальную программу-калькулятор для расчета.
Для начала следует замерить пролет, который вы хотите перекрыть деревянными балками, а после уделить особое внимание способу фиксации. Очень важно, как глубоко будут заходить в стену фиксирующие элементы. Только после проведения всех подобных операций вы сможете заняться расчетом несущей способности и прогиба деревянных балок и остальных параметров, которые не менее важны при строительстве.
Длина
Перед началом расчета прогиба и несущей способности узнайте, какова длина каждой доски из дерева. Такой параметр определен длиной пролета, и все же это еще не все. Все подсчеты должны быть выполнены с определенным запасом.
Обратите внимание, что, если деревянные балки будут заделаны в стены, это будет влиять на их длину и остальные расчеты.
Материал
При проведении подсчета немаловажное значение имеет материал, из которого вы хотите построить дом. Если вы выбрали в качестве основного материала кирпич, доски должны будут быть вмонтированы в гнезда, и приблизительная глубина при этом должна быть от 10 до 15 см. если же речь идет о постройке из дерева, параметры, которые описаны в СНиП, кардинально меняются. В таком случае будет достаточно глубины в 7-9 см. Но учтите, что из-за этого изменится конечная несущая способность.
Если при монтаже будут использованы кронштейны или хомуты, то длина досок и бревен должна соответствовать проему. Если говорить проще, вам нужно рассчитать расстояние от одной стены до другой и тогда вы узнаете, какова несущая способность конструкции в целом.
Важно! При создании ската крыши за стены следует выносить бревна на 0,3-0,5 метра. Это обязательно нужно будет учитывать при подсчете способности конструкции противостояния различным нагрузкам.
Но не все зависит от того, что хочет воплотить архитектор, если дело касается одной лишь математики. Для обрезной доски допустима максимальная длина в 600 см., иначе несущая способность ухудшится и прогиб станет только больше.
Клееный брус
Не редкость, что у домов есть пролеты от 10 до 12 метров. Для осуществления этого используют клееный брус. Он бывает прямоугольным или двутавровым. Еще для надежности можно использовать опоры, и для этого идеально подойдут колоны или дополнительные стены.
Полезный совет! Большинство строителей, если требуется перекрыть длинный пролет, используют фермы.
Методология расчета – общая информация
При расчете деревянной балки на прогиб следует помнить, что для малоэтажного строительства не редкость использование однопролетных балок. Длина всех элементов может быть разной и в большом диапазоне. Чаще всего она зависит от того, какие параметры строения, которое вы хотите возвести.
Обратите внимание, что калькулятор на расчет деревянной балки на прогиб, который есть в конце этой статьи, даст возможность высчитать каждое из значений без временных затрат. Для использования программы введите все известные базовые данные.
В качестве несущих элементов конструкции используют деревянные бруски, у которых высота сечения от 14 до 25 см, а толщина от 5,5 до 15,5 см. Эти параметры используются чаще всего при расчете. Очень часто строители-профессионалы для усиления конструкции используют такое прекрасное дополнение, как перекрестная схема монтажа балок. Такая методика дает самые лучшие результаты при небольших временных и материальных затратах.
Если рассмотреть длину идеального пролета при выведении значения несущей способности деревянных балок, то ограничьте фантазию вашего архитектора параметрами от 2,5 до 4 метров.
Важно! Оптимальным вариантом сечения для деревянной балки считается та площадь, у которой соотношение высоты к ширине как 1,5 к 1.
Расчет прогиба и несущей способности
Хочется отметить, что за много лет строительства был выработан следующий алгоритм расчета, который используют чаще всего для расчета несущей способности деревянных балок: М/W<=Rд
В этой формуле значения переменных таковы:
- Буква М – это изгибающий момент, который измеряется к кг/с*м.
- W является значением момента сопротивления, и его единица измерения – это см3.
Расчет прогиба – это та часть, указанная выше формулы, и на этот показатель указывает переменная М. для того, чтобы узнать этот параметр, используют такую формулу: М=(ql2)/8
В этой формуле для расчета есть две основные переменные, но они и определяют какова будет несущая способность балки из дерева:
- Обозначение q указывает на нагрузку, которую доска в состоянии выдержать.
- А вот буква l является длиной одной из деревянных балок.
Обратите внимание,
что расчет прогиба и несущей способности деревянной балки во многом зависит от выбранного материала и метода его обработки.
Насколько важны параметры расчета
Описанные выше параметры очень важны для прочности конструкции в целом. Все дело в том, что одно й лишь стойкости бруса не хватит для обеспечения надежной и долгой службы, так как со временем прогиб из-за нагрузки может возрасти.
А он, в свою очередь, не просто будет портить красивый внешний вид перекрытия. Если этот параметр будет больше, чем 0,004 об всей длины перекрытия, то вероятность образования аварийного положения возрастает в несколько десятков раз.
Для чего нужен калькулятор
Установленный ниже калькулятор поможет рассчитать прогиб за пару секунд, а также несущую способность балки из дерева и многие другие параметры. С вас лишь требуется ввести данные, и вы мгновенно получите все расчеты по вашему будущему дому.
ТОП 9 магазинов, где я выгодно закупаюсь
ТОП 7 по товарам и мебели для дома:
7 лучших строительных и мебельных магазинов!
- Akson.ru- это интернет-гипермаркет строительных и отделочных материалов!
- homex.ru- HomeX.ru предлагает большой выбор качественных отделочных, материалов, света и сантехники от лучших производителей с быстрой доставкой по Москве и России.
- Instrumtorg.ru – это интернет – магазин строительного, автомобильного, крепежного, режущего и другого инструмента, необходимого каждому мастеру.
- Qpstol.ru — «Купистол» стремится предоставить лучший сервис своим клиентам. 5 звёзд на ЯндексМаркет.
- Lifemebel.ru- гипермаркет мебели с оборотом более 50 000 000 в месяц!
- Ezakaz.ru- Представленная на сайте мебель изготавливается на собственной фабрике в Москве, а так же проверенными производителями из Китая, Индонезии, Малайзии и Тайваня.»
- Mebelion.ru- – крупнейший интернет-магазин по продаже мебели, светильников, интерьерного декора и других товаров для красивого и уютного дома.
domsdelat.ru
Выполнение расчета прогиба деревянной балки
При действии нагрузки деревянные балки могут получать довольно большие прогибы, в результате которых нарушается их нормальная эксплуатация. Поэтому кроме расчетов по первой группе предельных состояний (прочность), необходимо выполнить расчет деревянных балок и по второй группе т. е.
по прогибам. Расчет деревянных балок на прогиб выполняется на действие нормативных нагрузок. Нормативную нагрузку получаем разделением расчетной нагрузки на коэффициент надежности по нагрузке.
Вычесление нормативной нагрузки выполнятся в сервисе расчет деревянных балокавтоматически. Нормальная эксплуатация балок возможна, в случае если расчетный прогиб деревянной балки не превышает прогиб, установленный нормами. Нормативными документами установлены конструктивные и эстетико-психологические требования.
1. Конструктивные требования к прогибам деревянных балок.
Представлены в СП64.13330.2011 “ДЕРЕВЯННЫЕ КОНСТРУКЦИИ” Таблица 19Элементы конструкцийПредельные прогибы в долях пролета, не более1 Балки междуэтажных перекрытий 2 Балки чердачных перекрытий 3 Покрытия (кроме ендов): а) прогоны, стропильные ноги б) балки консольные в) фермы, клееные балки (кроме консольных) г) плиты д) обрешетки, настилы 4 Несущие элементы ендов 5 Панели и элементы фахверха1/2501/2001/2001/1501/3001/250 1/1501/4001/250
1. Эстетическо-психологические требования к прогибам деревянных балок.
Представлены в СП20.13330.2011 “НАГРУЗКИ И ВОЗДЕЙСТВИЯ” Приложение Е.2
Элементы конструкцийВертикальные предельные прогибы 2 Балки, фермы, ригели, прогоны, плиты, настилы (включая поперечные ребра плит и настилов):а) покрытий и перекрытий, открытых для обзора, при пролете l, м: l<1 l<3 l<6 l<12 l<24 1/1201/150 1/2001/2501/300В случае если балка скрыта (к примеру, под подшивным потолком) то соблюдение эстетико-психологических требований не является обязательным. В данном случае необходимо выполнить расчет прогибов балкина соблюдение только конструктивных требований по прогибам.
Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.
Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.
Что нужно для того чтобы сделать правильный расчёт
Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.
Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками.
Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.
Длина
Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски.
Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.
Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.
При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.
Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.
Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.
Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.
К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.
Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус.
Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.
Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.
Общая информация по методологии расчёта
В большинстве случаев в малоэтажном строительстве применяются однопролётные балки.
Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.
Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.
Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.
Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.
Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.
Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.
Как рассчитать несущую способность и прогиб
Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:
M/W<=Rд
Расшифруем значение каждой переменной в формуле:
- Буква Мвначале формулы указывает на изгибающий момент. Он исчисляется в кгс*м.Wобозначает момент сопротивления. Единицы измерения см3.
Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква Муказывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:
M=(ql2)/8
В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:
- Символ q показывает нагрузку, которую способна выдержать доска.В свою очередь буква l— это длина одной деревянной балки.
Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.
Насколько важно правильно рассчитать прогиб
Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.
Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.
Так зачем нужен калькулятор
Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.
В современном индивидуальном строительстве деревянные балки используются почти в каждом проекте. Найти постройку, в которой не используются деревянные перекрытия, практически невозможно. Деревянные балки применяются и для устройства полов, и в качестве несущих элементов, как опоры для межэтажных и чердачных перекрытий.
Формула расчета прогиба балки.
Известно, что деревянные балки, как и любые другие, могут прогибаться под воздействием различных нагрузок.
Эта величина — стрелка прогиба — зависит от материала, характера нагрузки и геометрических характеристик конструкции. Небольшой прогиб вполне допустим. Когда мы ходим, например, по деревянному настилу, то чувствуем, как пол слегка пружинит, однако если такие деформации незначительны, то нас это мало беспокоит.
Насколько можно допустить прогиб, определяется двумя факторами:
- Прогиб не должен превышать расчетных допустимых значений.Прогиб не должен мешать эксплуатации здания.
Чтобы узнать, насколько будут деформироваться деревянные элементы в конкретном случае, нужно произвести расчеты на прочность и жесткость. Подробные и детальные расчеты такого рода — это работа инженеров-строителей, однако, имея навык математических вычислений и зная несколько формул из курса сопротивления материалов, вполне можно самостоятельно рассчитать деревянную балку.
Вспомогательная таблица для расчета количества балок.
Любая постройка должна быть прочной.
Именно поэтому балки перекрытия проверяют в первую очередь на прочность, чтобы конструкция могла выдерживать все необходимые нагрузки, не разрушаясь. Кроме прочности конструкция должна обладать жесткостью и устойчивостью. Величина прогиба является элементом расчета на жесткость.
Прочность и жесткость неразрывно связаны между собой. Вначале делают расчеты на прочность, а затем, используя полученные результаты, можно сделать расчет прогиба.
Чтобы правильно спроектировать собственный загородный дом, необязательно знать полный курс сопротивления материалов. Но углубляться в слишком подробные вычисления не стоит, как и просчитывать различные варианты конструкций.
Чтобы не ошибиться, лучше воспользоваться укрупненными расчетами, применяя простые схемы, а высчитывая нагрузки на несущие элементы, всегда делать небольшой запас в большую сторону.
Алгоритм вычисления прогиба
Рассмотрим упрощенную схему расчета, опуская некоторые специальные термины, и формулы для расчета двух основных случаев нагружения, принятых в строительстве.
Нужно выполнить следующие действия:
- Составить расчетную схему и определить геометрические характеристики балки.Определить максимальную нагрузку на этот несущий элемент.При необходимости проверить брус на прочность по изгибающему моменту.Вычислить максимальный прогиб.
Расчетная схема балки и момент инерции
Расчетную схему сделать довольно просто. Нужно знать размеры и форму поперечного сечения элемента конструкции, способ опирания, а также пролет, то есть расстояние между опорами. Например, если вы укладываете опорные брусья перекрытия на несущие стены дома, а расстояние между стенами 4 м, то пролет будет l=4 м.
Деревянные балки рассчитывают как свободно опертые. Если это балка перекрытия, то принимается схема с равномерно распределенной нагрузкой q. В случае если нужно определить изгиб от сосредоточенной нагрузки (например, от небольшой печки, выложенной прямо на перекрытии), принимается схема с сосредоточенной нагрузкой F, равной весу, который будет давить на конструкцию.
Для определения величины прогиба f необходима такая геометрическая характеристика, как момент инерции сечения J.
Схема монтажа деревянных балок перекрытий.
Для прямоугольного сечения момент инерции подсчитывается по формуле:
J=b*h^3/12, где:
b — ширина сечения;
h — высота сечения балки.
Например, для сечения размером 15х20 см момент инерции будет равен:
J=15*20^3/12=10 000 см^4=0,0001 м^4.
Здесь нужно обратить внимание на то, что момент инерции прямоугольного сечения зависит от того, как оно сориентировано в пространстве. Если брус положить широкой стороной на опоры, то момент инерции будет значительно меньше, а прогиб — больше.
Этот эффект каждый может прочувствовать на практике. Все знают, что доска, положенная обычным способом, прогибается гораздо сильнее, чем та же доска, положенная на ребро. Это свойство очень хорошо отражается в самой формуле для вычисления момента инерции.
Определение максимальной нагрузки
Для определения максимальной нагрузки на балку нужно сложить все ее составляющие: вес самого бруса, вес перекрытия, вес обстановки вместе с находящимися там людьми, вес перегородок.
Все это нужно сделать в пересчете на 1 пог. м балки. Таким образом, нагрузка q будет состоять из следующих показателей:
Расчет на смятие опорных участков балки.
вес 1 пог.
м балки;вес 1 кв. м перекрытия;временная нагрузка на перекрытие;нагрузка от перегородок на 1 кв. м перекрытия.
Кроме того, нужно учесть коэффициент k, равный расстоянию между балками, измеренному в метрах.
Для упрощения подсчетов можно принять усредненный вес перекрытия 60 кг/м², принятую в строительстве нормативную временную нагрузку на перекрытие, равную 250 кг/м², нагрузку от перегородок по тем же нормативам 75 кг/м², вес деревянной балки можно вычислить, зная объем и плотность древесины.
Для сечения 0,15х0,2 м этот вес будет равен 18 кг/пог. м. Если расстояние между брусьями перекрытия равно 600 мм, то коэффициент k равен 0,6.
Подсчитываем: q=(60+250+75)*0,6+18=249 кг/м.
Перейдем к расчету величины максимального прогиба.
Расчеты максимального прогиба
Для рассматриваемого случая с равномерно распределенной нагрузкой максимальный прогиб рассчитывается по формуле:
f=-5*q*l^4/384*E*J.
В этой формуле величина Е — это модуль упругости материала. Для древесины Е=100 000 кгс/м².
Подставляя полученные ранее величины, получаем, что максимальный прогиб деревянной балки сечением 0,15х0,2 м и длиной 4 м будет равен 0,83 см.
Если принять расчетную схему с сосредоточенной нагрузкой, то формула для подсчета прогиба будет другая:
f=-F*l^3/48*E*J, где:
F — сила давления на брус, например, вес печи или другого тяжелого оборудования.
Модуль упругости Е для разных видов древесины различен, эта характеристика зависит не только от породы дерева, но и от вида бруса — цельные балки, клееный брус или оцилиндрованное бревно имеют различные модули упругости.
Подобные вычисления могут производиться с различными целями. Если вам нужно просто узнать, в каких пределах будут находиться деформации элементов конструкции, то после определения стрелки прогиба дело можно считать завершенным. Но если вас интересует, насколько полученные результаты соответствуют строительным нормам, то необходимо выполнить сравнение полученных результатов с цифрами, приведенными в соответствующих нормативных документах.
Балка является основным элементом несущей конструкции сооружения.
При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.
При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах.
Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно.Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.
Виды балок
Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению.
Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.
Деревянные
Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.
Для расчета максимального прогиба следует учитывать:
- Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.Форма поперечного сечения и другие геометрические характеристики.Различные виды нагрузки на материал.
Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.
Конструкции из древесины хвойных пород
Стальные
Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.
Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:
- электросварка;заклепки;болты, винты и другие виды резьбовых соединений.
Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.
Для проведения расчета балки на прогиб может помочь видео:
Прочность и жесткость балки
Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.
Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали.
Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.
Существует два основных метода расчета прочности и жесткости:
- Простой. При использовании данного метода применяется увеличительный коэффициент.Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.
Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.
Расчет на жесткость
Для расчета прочности балки на изгиб применяется формула:
Где:
M – максимальный момент, который возникает в балке;
Wn,min– момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.
Ryявляется расчетным сопротивлением стали при изгибе. Зависит от вида стали.
γcпредставляет собой коэффициент условий работы, который является табличной величиной.
Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:
- Составление расчетной схемы объекта.Расчет размеров балки и ее сечения.Вычисление максимальной нагрузки, которая воздействует на балку.Определение точки приложения максимальной нагрузки.Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.Вычисление значения жесткости или максимально прогиба балки.
Чтобы составить расчетную схему, потребуются такие данные:
- размеры балки, длину консолей и пролет между ними;размер и форму поперечного сечения;особенности нагрузки на конструкцию и точно ее приложения;материал и его свойства.
Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.
Расчет моментов инерции и сопротивления сечения
Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:
Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.
Определение максимальной нагрузки и прогиба
Для точного определения прогиба балки, лучше всего применять данную формулу:
Где:
q является равномерно-распределенной нагрузкой;
E – модуль упругости, который является табличной величиной;
l – длина;
I – момент инерции сечения.
Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.
Особенности расчета на прогиб
Расчет на прогиб проводится обязательно для любых перекрытий.
Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:
- Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.Варианты нагружения консольного стержня, который закреплен жестко.Действие на конструкцию сложной нагрузки.
Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.
Пример подсчета прогиба
Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:
- материал изготовления – древесина;плотность составляет 600 кг/м3;длина составляет 4 м;сечение материала составляет 150*200 мм;масса перекрывающих элементов составляет 60 кг/м²;максимальная нагрузка конструкции составляет 249 кг/м;упругость материала составляет 100 000 кгс/ м²;J равно 10 кг*м².
Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:
- вес одного метра балки;вес м2 перекрытия;расстояние, которое оставляется между балками;временная нагрузка;нагрузка от перегородок на перекрытие.
Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.
Если подставить все эти значения в формулу, то получится:
q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.
Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].
Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.
Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.
Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины.
Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид.
Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.
Источники:
- rascheta.net
- bouw.ru
- 1poderevu.ru
- viascio.ru
blog-potolok.ru
| Двутавровая балка GreenLum-300L | Брус сухой строганный деревянный 100х240 мм | Цельный прямоугольный LVL брус 69х260 |
|---|---|---|
| Характеристики: Момент инерции 9 476,5 см4 Момент сопротивления 631,8 см3 Модуль упругости 12 000 МПа Расчетное сопротивление 22,0 МПа | Характеристики: Момент инерции 11 520,0 см4 Момент сопротивления 960,0 см3 Модуль упругости 9 000 МПа Расчетное сопротивление 14,0 МПа | Характеристики: Момент инерции 8 788,0 см4 Момент сопротивления 676,0 см3 Модуль упругости 14 000 МПа Расчетное сопротивление 26,5 МПа |
|
Производим расчет по первому предельному состоянию: (где, R — расчетное сопротивление изгибу, M-максимальный момент (M=q*L2/8; M=160*5,82/8=672,8 кНм), W-момент сопротивления) | ||
| R=M/W R=672,8 кНм/631,8*10-6 см3= 1,06 кНм2 = 10,6 МПа < Rрасч =22 МПа Выполнено. | R=M/W R=672,8 кНм/960*10-6 см3= 0,7 кНм2 = 7 МПа < Rрасч =14 МПа Выполнено. | R=M/W R=672,8 кНм/676*10-6 см3= 0,99 кНм2 = 9,9 МПа < Rрасч =26,5 МПа Выполнено. |
|
Производим расчет по второму предельному состоянию: (f/L < fпред/L | ||
| f/L=5*160*5,83 / (384*12000*105*9476,5*10-8)=0,00358 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*11520*10-8)= 0,00392 <fпред/L=0,004 Выполнено. | f/L=5*160*5,83/ (384*9000*105*8788*10-8)= 0,00392 <fпред/L=0,004 Выполнено. |
| Вывод: все 3 материала с данными геометрическими характеристиками примерно равны по своей несущей способности и удовлетворяют условиям прогибов. | ||
| Сравним цены и эксплуатационные характеристики | ||
|
|
|
enter-city.ru
Расчёт деревянных балок перекрытия. Калькулятор. – Копилка идей
Расчёт лаг для крыши, пола, покрытий деревянных конструкций.
Для расчёта необходимо знать снеговую нагрузку в регионе. Снеговая нагрузка для Удмуртии 320 кг/м.
Самый продвинутый калькулятор расчёта деревянных балок перекрытия …
http://vladirom.narod.ru/stoves/beamcalc.html
Основными несущими конструкциями деревянного перекрытия являются балки. Они воспринимают нагрузку собственного веса, заполнения, а также эксплуатационные нагрузки, передавая их на прогоны или столбы.
Балки (лаги), обычно из сосны, ели, лиственницы, для междуэтажных и чердачных перекрытий должны быть сухими (допустимая влажность не более 14%; при правильном хранении древесина приобретает такую влажность через год). Чем суше балка, тем она прочнее и тем меньше прогибается от нагрузки.
Балки не должны иметь пороков, влияющих на их прочностные характеристики (большое число сучков, косослой, свилеватость и т.д.). Балки подвергают обязательному антисептированию и противопожарной пропитке.
Если половые балки первого этажа опираются на столбики, поставленные довольно часто, то балки междуэтажных и чердачных перекрытий опираются на стены только своими концами и редко, когда под ними ставят опоры. Чтобы междуэтажные балки не прогибались, их следует тщательно рассчитать и укладывать на расстоянии 1 м друг от друга, а то и ближе.
Самая прочная на изгиб балка — это брус с соотношением сторон 7:5, т. е. высота балки должна равняться семи каким-то мерам, а ширина — только пяти таким же мерам. Круглое бревно выдерживает бОльшую нагрузку, чем вытесанный из него брус, однако оно менее прочно на изгиб.
Обычно балки прогибаются от давления на них веса засыпки, пола, мебели, людей и т.д. Прогиб в основном зависит от высоты балки, а не от ее ширины. Если, например, два одинаковых бруса скрепить болтами и шпонками, то такая балка выдержит груз уже в два раза больший, чем оба эти бруса, уложенные рядом. Поэтому выгоднее увеличивать высоту балки, чем ее ширину. Однако и в уменьшении ширины есть свой предел. Если балка будет слишком тонкой, то она может изогнуться в сторону.
Допустим, что прогиб балок междуэтажных перекрытий считается не более 1/300 длины перекрываемого пролета, чердачных — не более 1/250. Если перекрывается чердак пролетом 9 м (900 см), то прогиб не должен быть более 3,5 см (900:250=3,5 см). Зрительно это почти незаметно, но прогиб все же есть.
Любое перекрытие, даже под нагрузкой, будет совершенно ровным, если в укладываемых балках предварительно вытесать так называемый строительный подъем. В этом случае нижней стороне каждой балки придают форму плавной кривой с подъемом в середине (рис. 1).
Рис. 1 Строительный подъем балки (размеры в см)Сначала потолок с такими балками будет слегка приподнятым в середине, но постепенно от нагрузки выровнится и станет почти горизонтальным. С той же целью для балок можно применять изогнутые в одну сторону бревна, соответственно подтесывая их.
Толщина балок для междуэтажных и чердачных перекрытий должна равняться не менее 1/24 ее длины. Например, устанавливается балка длиной 6 м (600 см). Значит, толщина ее должна составлять: 600:24=25 см. Если необходимо вытесать прямоугольный брус с соотношением сторон 7:5, берут уже бревно диаметром 30 см.
Брус можно заменить двумя досками общим сечением, равным брусу. Такие доски обычно сбивают гвоздями, располагая их в шахматном порядке через 20 см.
При более частой укладке вместо бревен (брусьев) можно использовать обыкновенные толстые доски, поставленные на ребро.
Рассмотрим такой пример. Для перекрытия пролета длиной 5 м с нагрузкой в 1259 кг необходимы две балки прямоугольного сечения 200X140 мм, уложенные через 1000 мм. Однако их можно заменить тремя досками сечением 200Х70 мм, расположив их через 500 мм, или же четырьмя досками сечением 200Х50 мм, уложенными через 330 мм (рис. 2).
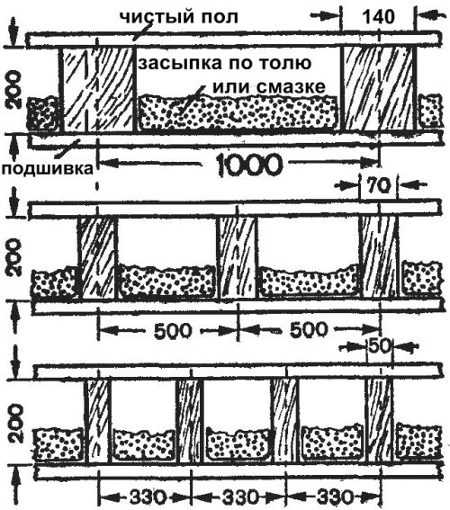
Дело в том, что доска сечением 200X70 мм выдерживает груз 650 кг, сечением 200X50 мм – 420 кг. В сумме же они будут выдерживать предполагаемую нагрузку.
Для подбора сечения круглых или прямоугольных балок под нагрузку 400 кг на 1м2 перекрытия можно пользоваться данными таблицы или приведенными расчетами.
Допустимые сечения балок междуэтажных и чердачных перекрытий в зависимости от пролета при нагрузке 400 кг
| Ширина пролета (м) | Расстояние между балками (м) | Диаметр бревен (см) | Сечение брусков (высота на ширину, см) |
| 2 | 1 | 13 | 12×8 |
| 0,6 | 11 | 10×7 | |
| 2,5 | 1 | 15 | 14×10 |
| 0,6 | 13 | 12×8 | |
| 3 | 1 | 17 | 16×11 |
| 0,6 | 14 | 14×9 | |
| 3,5 | 1 | 19 | 18×12 |
| 0,6 | 16 | 15×10 | |
| 4 | 1 | 21 | 20×12 |
| 0,6 | 17 | 16×12 | |
| 4,5 | 1 | 22 | 22×14 |
| 0,6 | 19 | 18×12 | |
| 5 | 1 | 24 | 22×16 |
| 0,6 | 20 | 18×14 | |
| 5,5 | 1 | 25 | 24×16 |
| 0,6 | 21 | 20×14 | |
| 6 | 1 | 27 | 25×18 |
| 0,6 | 23 | 22×14 | |
| 6,5 | 1 | 29 | 25×20 |
| 0,6 | 25 | 23×15 | |
| 7 | 1 | 31 | 27×20 |
| 0,6 | 27 | 26×15 | |
| 7,5 | 1 | 33 | 30×27 |
| 0,6 | 29 | 28×16 |
Концы балок междуэтажных и чердачных перекрытий деревянных зданий врубают сковороднем в верхние венцы на всю толщину стены.
Для выбора балок можно также воспользоваться таблицей, разработанной И.Стояновым.
Подбор деревянных балок перекрытия
| Нагрузки, кг/пог.м | Сечение балок при длине пролета, м | ||||||
| 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | |
| 150 | 5×14 | 5×16 | 6×18 | 8×18 | 8×20 | 10×20 | 10×22 |
| 200 | 5×16 | 5×18 | 7×18 | 7×20 | 10×20 | 12×22 | 14×22 |
| 250 | 6×16 | 6×18 | 7×20 | 10×20 | 12×20 | 14×22 | 16×22 |
| 350 | 7×16 | 7×18 | 8×20 | 10×22 | 12×22 | 16×22 | 20×00 |
Нагрузки на перекрытия складываются из их собственной массы и временных нагрузок, возникающих в процессе эксплуатации дома. Собственная масса междуэтажных деревянных перекрытий зависит от конструкции перекрытия, применяемого утеплителя и обычно составляет 220-230 кг/м2, чердачных – в зависимости от массы утеплителя – 250-300 кг/м2. Временные нагрузки на чердачное перекрытие принимаются за 100 кг/м2, на междуэтажное – 200 кг/м2. Для того чтобы определить полную нагрузку, приходящуюся на один квадратный метр перекрытия в процессе эксплуатации дома, складывают временную и собственную нагрузки и их сумма является искомой величиной.
Наиболее экономичными по расходу древесины считаются балки толщиной 5 и высотой 15-18 см при расстоянии между ними 40-60 см и минераловатном утеплителе.
Вот таблица расчёта чердака холодного.
Максимальные пролёты балок чердачного перекрытия. Неэксплуатируемый чердак.Читайте также: Новости Новороссии.
sagalaeved.ru
Расчет деревянной балки перекрытия согласно СП 64.13330.2011
Итак планируется междуэтажное перекрытие по деревянным балкам для дома, имеющего следующий план:
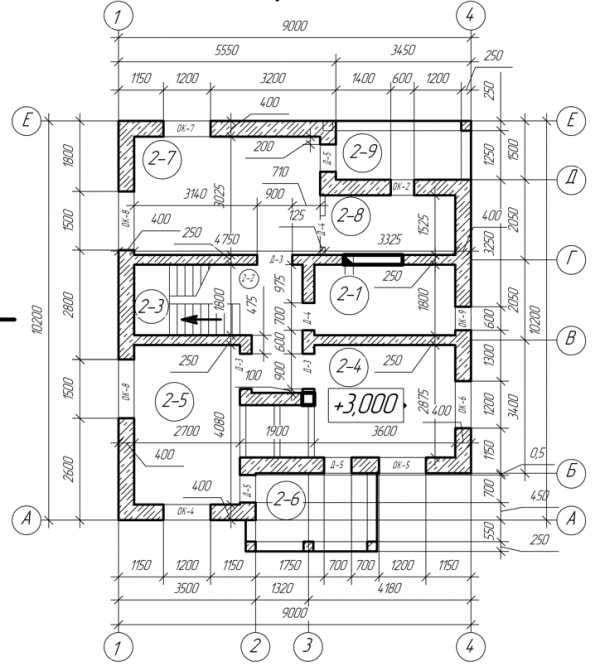
Рисунок 515.1. План помещений второго этажа.
1. Общий Расчет балки перекрытия санузла на прочность
Для того, чтобы рассчитать деревянную балку на прочность согласно требований СП, следует сначала определить множество различных данных на основании общих положений расчета балок.
1.1. Виды и количество опор
Деревянные балки будут опираться на стены. Так как мы не предусматриваем никаких дополнительных мер, позволяющих исключить поворот концов балки на опорах, то опоры балки следует рассматривать, как шарнирные (рисунок 219.2).
Рисунок 219.2.
Примечание: Так как концы балок, опирающиеся на каменные стены, для уменьшения риска гниения балок как правило обрабатывают гидроизоляционными материалами, имеющими относительно малый модуль упругости, при этом глубина заделки концов балки в стену не превышает 15-20 см, то даже если на опорные участки таких балок будет опираться каменная кладка, то это все равно не позволяет рассматривать такое опирание, как жесткое защемление.
1.2. Количество и длина пролетов
Согласно плану, показанному на рисунке 515.1, для перекрытия в санузле (помещение 2-1) длина пролета будет составлять около:
l = 4.18 — 0.4 = 3.78 м
При этом балки будут однопролетными, а значит статически определимыми.
1.3. Система координат
Расчет будем производить используя стандартную систему координат с осями х, у и z. При этом балка рассматривается как стержень, нейтральная ось которого совпадает с осью координат х, а начало координат совпадает с началом балки. Соответственно длина балки измеряется по оси х.
1.4. Действующие нагрузки
Все возможные расчетные плоские нагрузки для такого перекрытия мы уже собрали:
qрп = 212.46 кг/м2
qрв = 195 кг/м2
Примечание: при объемной чугунной ванне, установленной посредине балок перекрытия, расчетное значение временной нагрузки может быть значительно больше.
Однако такие значения нагрузок можно использовать только при расчете монолитного перекрытия. В нашем же случае балки перекрытия представляют собой крайние или промежуточные опоры для многопролетных балок — досок настила и остального пирога перекрытия.
Таким образом для более точного определения нагрузки на наиболее загруженную балку следует точно знать, доски какой длины будут использоваться в качестве настила по балкам. Если такого знания нет, то я рекомендую рассматривать наиболее неблагоприятный вариант, а именно — доски будут перекрывать 2 пролета, т.е. опираться на 3 балки перекрытия.
В этом случае наиболее нагруженной будет балка — промежуточная опора для таких досок — двухпролетных балок, соответственно значения нагрузок для такой балки следует увеличить в 10/8 = 1.25 раза или на 25%, тогда:
qрп = 212.46·1.25 = 265.58 кг/м2
qрв = 195·1.25 = 243.75 кг/м2
Если доски будут перекрывать 3 пролета, то значения нагрузок следует увеличить в 1.1 раза (253.4.4). При 4 пролетах — в 8/7 = 1.15 раза (262.7.10) и так далее, тем не менее остановимся на первом варианте, так оно надежнее.
Так как на рассчитываемое перекрытие действует только одна кратковременная нагрузка (особые нагрузки типа взрывной волны или землетрясения мы для нашего перекрытия не предусматриваем), то при рассмотрении основного сочетания нагрузок используется полное значение кратковременной нагрузки согласно СП 20.13330.2011 «Нагрузки и воздействия» п.1.12.3, тогда:
qр = 265.58 + 243.75 = 509.33 кг/м2
Так как балки рассчитываются не на плоскую, а на линейную нагрузку, то при шаге балок 0.6 м расчетная линейная нагрузка на балку составит:
qрл = 509.33·0.6 = 305.6 кг/м
1.5. Определение опорных реакций и максимального изгибающего момента
Так как загружение балки равномерно распределенной нагрузкой — достаточно распространенный частный случай, то для определения опорных реакций можно воспользоваться готовыми формулами:
А = В = ql/2 = 305.6·3.78/2 = 577.6 кг
Мmax = ql2/8 = 305.6·3.782/8 = 545.82 кгм или 54582 кгсм
1.6. Построение эпюр поперечных сил и изгибающих моментов
В нашем частном случае, когда нагрузка является равномерно распределенной, можно опять же воспользоваться готовыми эпюрами, благо их для такого случая построено уже множество:
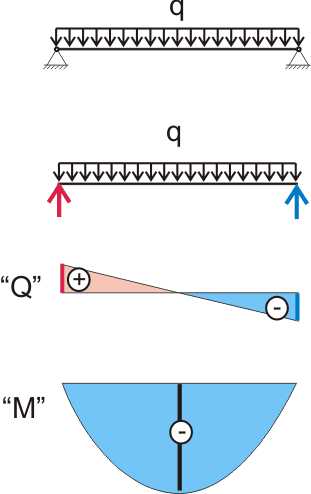
Рисунок 149.7.2. Эпюры поперечных сил и моментов, действующих в поперечных сечениях
Для большей наглядности можно нанести полученные значения поперечных сил (опорные реакции — это и есть значения поперечных сил в начале и в конце балки) и максимального изгибающего момента на эпюры.
Примечание: В данном случае эпюра моментов помечена знаком минус, просто потому, что откладывается снизу от оси координат х. А вообще знак для моментов принципиального значения не имеет, так как при действии момента всегда есть и растянутая и сжатая зона поперечного сечения. Таким образом наиболее важно понимать, где при действии момента будет растянутая, а где сжатая зона сечения. Впрочем для деревянных балок это большого значения не имеет.
1.7. Определение требуемого момента сопротивления
Согласно СП 64.13330.2011 «Деревянные конструкции» п.6.9 расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования, следует производить, исходя из следующего условия:
M/Wрасч ≤ Rи (или Rид.ш.) (533.1)
где М — расчетное значение изгибающего момента. В нашем случае (для балки постоянного сечения при действии равномерно распределенной нагрузки) достаточно проверить балку на действие максимального изгибающего момента. В общем случае при достаточно сложной комбинации различных нагрузок или для балок переменного сечения могут потребоваться проверки на прочность в нескольких сечениях. Для определения момента в этих сечениях и используется эпюра моментов.
Rи — расчетное сопротивление древесины изгибу. Определение расчетного сопротивления древесины в зависимости от различных факторов — отдельная большая тема. В данном случае ограничимся тем, что при использовании балок из цельной древесины — сосны 2 сорта расчетное сопротивление изгибу для балок перекрытия санузла может составлять Rи = 113.3 кгс/см2.
Rид.ш. — расчетное сопротивление для элементов из однонаправленного шпона, но так как в данном случае мы рассматриваем балку из цельной древесины, то возможные значения клееных элементов нас не интересуют
Wрасч— расчетный момент сопротивления рассматриваемого поперечного сечения. Для элементов из цельной древесины Wрасч = Wнт, где Wнт — момент сопротивления рассматриваемого сечения с учетом возможных ослаблений — момент сопротивления нетто.
Так как для рассчитываемых балок не предусматривается никаких ослаблений в зоне максимального загружения (гвозди крепления досок перекрытия не в счет), то требуемый по расчету момент сопротивления поперечного сечения балки можно определить, преобразовав соответствующим образом формулу (533.1):
Wрасч ≥ М/Rи = 54582/113.3 = 481.73 см3
1.8. Определение геометрических параметров сечения
Так как мы предварительно приняли прямоугольное поперечное сечение балок, имеющее размеры b — ширину и h — высоту, то задавшись значением одного из этих параметров, мы можем определить значение другого.
Если принять ширину балок 10 см, исходя из сортамента производимых в ближайших окрестностях лесоматериалов, то требуемую высоту поперечного сечения можно определить по формуле:
(147.4)
hтр = √6·481.73/10 = 17 см.
Исходя из все того же сортамента, высоту балок следует принять не менее 20 см. Также можно уменьшить шаг балок, например при шаге балок 0.45 м значение расчетного момента сопротивления составит не менее
Wрасч = 0.5·481.73/0.6 = 361.3 см3
и тогда минимально допустимая высота сечения
hтр = √6·361.3/10 = 14.72 см.
А значит можно принять высоту балок равной 15 см. Впрочем, возможны и другие варианты подхода, например, более точно учесть количество пролетов, перекрываемых досками, это позволит уменьшить значение нагрузки на 10-15%.
2. Определение прогиба
Так как для однопролетных балок с шарнирными опорами значение прогиба может стать определяющим, то я рекомендую определять прогиб сразу после определения параметров сечения.
При действии равномерно распределенной нагрузки на однопролетную балку с шарнирными опорами значение прогиба без учета влияния поперечных сил можно определить по следующей формуле:
f0 = 5ql4/(384EI)
где q — нормативное значение нагрузки.
Значения плоских нормативных нагрузок, необходимые для определения прогиба, мы уже определили при сборе нагрузок. Они составляют:
qнп = 171.6 кг/м2
qнв = 150 кг/м2
Соответственно с учетом шага балок 0.6 м и перераспределения опорных нагрузок линейная нормативная нагрузка составляет:
qнл = 0.6·1.25(171.6 + 150) = 241.2 кг/м (2.412 кг/см)
Е = 105 кгс/см2, модуль упругости древесины, принимаемый по СП 64.13330.2011 «Деревянные конструкции».
I = bh3/12 = 10·203/12 = 6666.67 см4, — момент инерции рассматриваемого прямоугольного сечения балки.
Тогда
f0 = 5·2.412·3784/(384·105·6666.67) = 0.962 см
При действии равномерно распределенной нагрузки на балку значение коэффициента с, учитывающего влияние поперечных сил на значение прогиба, составит согласно таблицы Е.3:
с = 15.4 + 3.8β (533.2)
Так как высота балки у нас постоянная величина, то β =1 = k и соответственно
с = 15.4 + 3.8 = 19.2
Тогда при высоте балки h = 0.2 м и пролете l = 3.78 м (h/l = 0.053) значение прогиба с учетом поперечных сил составит:
f = fo[1 + c(h/l)2]/k = 0.962[1 + 19.2·0.0532]/1 = 1.01 см
Предельно допустимое значение прогиба деревянных балок междуэтажного перекрытия согласно таблицы 19 СП 64.13330.2011 «Деревянные конструкции» составляет fд = l/250 = 387/250 = 1.55 см.
Необходимые требования по максимально допустимому прогибу нами соблюдены, мы можем продолжать расчет.
1.9. Проверка по касательным напряжениям (прочность по скалыванию)
При изгибе в сечениях, поперечных и параллельных нейтральной оси балки, будут действовать касательные напряжения. В деревянных балках это может привести к скалыванию древесины вдоль волокон. поэтому касательные напряжения т не должны превышать расчетного сопротивления Rск скалыванию:
т = QS’бр/bрасIбр ≤ Rск (Rскд.ш.) (533.3)
где Q — значение поперечной силы в рассматриваемом поперечном сечении, определяемое по эпюре моментов. В нашем случае максимальные касательные напряжения будут действовать на опорах балки, Q = 557.6 кг
S’бр — статический момент брутто (т.е. без учета возможных ослаблений сечения) сдвигаемой (скалываемой) части сечения. Статический момент определяется относительно нейтральной оси балки.
bрас — расчетная ширина сечения рассматриваемого элемента конструкции. В данном случае у нас ширина балки равна bрас = 10 см.
Rск — расчетное сопротивление древесины скалыванию. Как и при определении расчетного сопротивления изгибу значение, определенное по таблице 3, следует дополнительно умножить на ряд коэффициентов, учитывающих различные факторы. Впрочем факторы у нас не изменились и потому согласно п.5.а) и определенным ранее коэффициентам расчетное сопротивление скалыванию составит:
Rск = 1.6·0.9·0.95 = 1.368 МПа (13.95 кгс/см2)
Iбр — момент инерции брутто, т.е. опять же определяемый без учета возможных ослаблений сечения. В данном случае момент инерции брутто совпадает с определенным ранее моментом инерции.
Впрочем, для балок прямоугольного сечения нет большой необходимости при подобных расчетах определять как статический момент полусечения, так и момент инерции. По той причине, что максимальные касательные напряжения действуют посредине высоты балки и составляют:
т = 1.5Q/F (270.3)
Тогда
т = 1.5·557.6/(10·20) = 4.182 кг/см2 < 13.95 кг/см2
Требование по прочности по скалыванию соблюдается, причем с 3-х кратным запасом.
На этом расчет деревянной балки постоянного сплошного сечения, устойчивость которой из плоскости изгиба обеспечена другими элементами конструкции, можно считать законченным. Во всяком случае никаких дополнительных требований Сводом Правил в таких случаях не предъявляется.
Тем не менее я рекомендую дополнительно проверить опорные участки балки
1.10. Проверка на прочность опорных участков балки
Любая балка в отличие от показанной на рисунке 219.2 модели имеет опорные участки. На этих опорных участках действуют нормальные напряжения в сечениях, параллельных нейтральной оси балки.
Распределение нормальных напряжений на этом участке зависит от множества различных факторов, в частности от угла поворота поперечного сечения балки на опоре, длины опорных участков и т.п.
Если для упрощения расчетов принять линейное изменение нормальных напряжений от максимума до 0, то примерное значение максимальных нормальных напряжений на опорных участках можно определить по следующей формуле:
σу = 2Q/(blоп) ≤ Rcм90 (533.4)
где Q — значение поперечной силы согласно эпюры «Q», как и прежде оно составляет Q = 557.6 кг;
b — ширина балки b = 10 см;
lоп — длина опорного участка, из конструктивных соображений примем lоп = 10 см;
2 — коэффициент учитывающий неравномерность распределения напряжений на опорном участке;
Rcм90 — расчетное сопротивление смятию поперек волокон. Согласно п.4.а) таблицы 3 и с учетом поправочных коэффициентов расчетное сопротивление смятию поперек волокон составит:
Rсм90 = 4·0.9·0.95 = 3.42 МПа (34.8 кгс/см2)
Тогда
2·557.6/(10·10) = 11.15 кг/см2 < 34.8 кг/см2
Как видим условие по прочности на опорных участках также соблюдается и снова с хорошим 3-х кратным запасом.
И теперь расчет балки перекрытия санузла можно действительно считать законченным.
Дополнительные проверки на прочность в местах действия сосредоточенных нагрузок здесь не требуются как минимум потому, что при принятой расчетной схеме сосредоточенные нагрузки отсутствуют. Да и рассматривать плоское напряженное состояние балки для определения максимальных напряжений при постоянном сплошном прямоугольном сечении балки и принятой схеме нагрузок и опор на мой взгляд также не требуется.
doctorlom.com
Расчет деревянной балки перекрытия на прогиб, пример, таблица
Применяется и такое конструктивное решение, когда несущие элементы перекрытия являются частью стропильных конструкций. В этом случае балка является конструкцией для формирования свеса, то она опирается на мауэрлат и имеет выпуск за внешнюю грань каждой стены примерно на 500 мм. Это конструктивное решение может увеличить её длину примерно на 1 метр.
Производя подбор и расчет деревянных балок необходимо помнить, что самым оптимальным расстоянием, которое можно перекрывать, применяя эти конструктивные элементы, является 6 метровый пролет.
При необходимости перекрывать большие расстояния рекомендуется использование деревянных конструкций прямоугольного или двутаврового сечения изготовленных из клееного бруса или применять промежуточные конструкции, такие как стойки, колонны, декоративные арки и т.п.
Сбор нагрузок воздействующих на балки
Диапазон различного вида нагрузок действующих на несущие конструкции достаточно велик. Он различается исходя из целевого применения балки, то есть ответа на вопрос эта балка располагается в междуэтажном или чердачном перекрытии. Конструкции междуэтажных перекрытий несут нагрузку в основном только от веса самого перекрытия, от процесса жизнедеятельности людей которые там находятся и того производственного процесса который там проходит.
Так расчетная нагрузка на междуэтажное перекрытие в жилых зданиях равна 150кг/м2 х 1,3 = 195 кг/м2.
Коэффициент 1,3 обеспечивает надежность работы конструкции. Вес междуэтажного перекрытия включает вес балок, полов, конструкций потолка, утеплителя. При производстве расчетов вес междуэтажного перекрытия лучше всего рассчитывать в каждом случае индивидуально.
Нагрузка на чердачное перекрытие, эксплуатация которого не предусматривает 70 кг/м2 х 1,3 = 91 кг/м².
Вес самого чердачного перекрытия включает в себя вес балок, утеплителя, материала зашивки и составляет 50 кг/м2. В случае, если балка является не только чердачным перекрытием, но и входит в конструкцию стропильной системы здания, то её расчет производится в составе стропильных конструкций.
В случае, когда величина прогиба превышает указанные величины, это может нанести существенные деформационные изменения в геометрии потолочных конструкций. Так при длине балки перекрытия 6 метров величина допустимого прогиба будет составлять 17 мм. Если предположить, что потолок в помещении будет из гипсокартонных плит, то образование трещин неминуемо. Поэтому производя расчет, следует сразу же учитывать материал, из которого будет выполняться конструкция потолка. Если заказчик для оформления потолка будет использовать подвесные конструкции типа «Армстронг», то беспокоиться не о чем, а если для отделки будут применяться материалы на основе гипса, минеральных вяжущих, то возможно стоит увеличить надежность перекрытия и увеличить сечение балок, чтобы полностью исключить возможность прогиба.
opotolkax.com
Расчет деревянного перекрытия | Все о ремонте и строительстве
Сначала о нагрузках. По таблице 3.3 СНиП 2.01.07-85* временная нагрузка на перекрытие считается равной 150 кг/м². То есть на каждом квадратном метре перекрытия можно будет разместить 150 кг дополнительного веса сверх постоянных нагрузок. К постоянным нагрузкам относят вес самого перекрытия с напольными конструкциями и вес межкомнатных перегородок. Мебель, санитарно-техническое оборудование и вес людей относят к временным нагрузкам.
Какую величину нагрузки выбрать для устройства деревянного перекрытия? Проще всего провести аналогию с чем-то хорошо знакомым. Например, в наших квартирах используются железобетонные перекрытия с несущей способностью от 400 до 800 кг/м². В последнее время применяются в основном плиты перекрытия с несущей способностью 800 кг/м². Стоит ли принимать к расчету деревянного перекрытия такую нагрузку? Наверное, нет. Как показывает практика, нагрузка на перекрытие чаще всего, не превышает 350–400 кг/м². Однако это не исключает того, что вы, проектируя перекрытие под свои конкретные нужды, примите другую величину нагрузки. В любом случае, все возможные нагрузки лучше учесть заранее и спроектировать перекрытие с небольшим (не более 40%) запасом прочности, чем потом, при возникшей необходимости, заниматься его упрочнением.
Для подбора сечений балок перекрытия, нагрузку исчисляемую в килограммах на квадратный метр нужно перевести в нагрузку, на погонный метр длины балки. Мы легко можем представить себе, например, квадратный лист железа со сторонами длинной в 1 м. Если мы надавим на этот лист весом в 400 кг и подложим под его середину деревянную балку, то на один метр длинны этой балки будет давить сила 400 кг. Это очевидно. А если мы подложим под лист две балки и распределим их под серединами половин листа, то на метр длины балок будет давить вес по 200 кг. Это тоже очевидно. Положив под лист три балки и равномерно раздвинув их, получим нагрузку на каждую балку уже по 133 кг. Таким образом, изменяя количество балок расположенных под одним квадратным метром, мы можем изменять давящую на них нагрузку и тем самым уменьшать сечение балок. Либо наоборот, разместить под двумя (тремя, четырьмя и т.д.) квадратными метрами одну балку и увеличить ее сечение.
Балки перекрытия рассчитываются не только по несущей способности, но еще и на прогиб. Жить в доме, в котором над головой прогнулось перекрытие, будь оно хоть трижды прочным — неприятно. Нормативная величина прогиба балки не должна превышать 1/250 ее длины.
Несущая способность древесины известна, сечения и длины балок то же не составляют тайны — их тысячи раз просчитывали до нас. Поэтому для определения сечения балок при известном пролете (длине от опоры до опоры) можно применить график изображенный на рисунке 37. При использовании графика нужно задать нагрузку и ширину балки и по ним определить ее высоту, для данного пролета балки. Либо зная длину пролета балки и размеры ее сечения, определить какую нагрузку она может выдержать. Изменяя шаг установки балок добиться требуемой величине нагрузки.
рис. 37. График для определения сечений деревянных балокГрафик предназначен для расчета однопролетных балок, т. е. балок лежащих на двух опорах. Также можно использовать калькулятор для расчета деревянных балок. Если будут применены двухпролетные балки (на трех опорах) или балки нестандартной длины, то можно попробовать программу для расчета наслонных стропил. Методика расчета балок и стропил почти одинакова. Правда, используя эту или другие подобные компьютерные программы нужно хотя бы понимать, что делаешь. В противном случае, лучше обратиться к инженерам-конструкторам.
ostroykevse.com
